Beispiel 8.2Übungen zur medizinischen Biometrie
- parametrische Tests
- nichtparametrische Tests
- Einstichprobentests
- Zweistichprobentests
- Mehrstichprobentests
- verbundene und unverbundene Stichproben
- t-Tests
- Mann-Whitney-Wilcoxon-Test
- Chi-Quadrat-Test auf Unabhängigkeit
- Logrank-Test
8.2 Klassifikation der Testverfahren
Um Anwendern die Suche nach dem richtigen statistischen Test zu erleichtern, sind die Tests grob nach verschiedenen Kriterien geordnet.
· Nach der Anzahl der zu vergleichenden Stichproben unterscheidet man Ein-, Zwei- und Mehrstichprobentests.
· Bei Zwei- und Mehrstichprobentests unterscheidet man weiter nach verbundenen und unverbundenen Stichproben.
Zwei Stichproben heißen unverbunden, wenn sowohl die Daten innerhalb einer Stichprobe als auch die Daten aus beiden Stichproben zusammen alle unabhängig voneinander sind.
Zwei Stichproben heißen verbunden, wenn es zu jedem x aus der einen Stichprobe genau ein y aus der anderen Stichprobe gibt, mit dem es inhaltlich ein Paar bildet. Verbundene Stichproben müssen daher stets den gleichen Stichprobenumfang haben. Man nennt zwei verbundene Stichproben auch paarige Stichproben.
Es ist unzulässig, ein Mehrstichprobenproblem mit mehr als zwei Stichproben durch mehrfaches Anwenden eines Zweistichprobentests zu lösen, denn dies würde die Irrtumswahrscheinlichkeit in unkontrollierter Weise vergrößern. Man muss auf die entsprechenden Mehrstichprobentests zurückgreifen.
· Nach Art der zu prüfenden Hypothese unterscheidet man parametrische und nichtparametrische Tests. Mit parametrischen Tests werden Hypothesen über den Parameter einer gegebenen Verteilung geprüft. Mit nichtparametrischen Tests werden Hypothesen über eine Verteilung als Ganzes geprüft.
Das Prinzip des statistischen Tests wurde bereits in Kapitel 6 am Beispiel des Vorzeichen- und des Wilcoxontests erläutert.
Im Beispiel 6.3 und 6.4 wurden Hämoglobinwerte von Patienten vor und nach Behandlung mit dem Vorzeichen- bzw. dem Wilcoxontest verglichen. Die Stichproben sind verbunden, denn zu jedem Wert aus der Stichprobe vor Behandlung gehört genau ein Wert aus der Stichprobe nach Behandlung. Das ist der Wert, der von dem gleichen Patienten stammt.
Der Vorzeichen- und der Wilcoxontest werden zu den nichtparametrischen Tests gezählt. Den Vorzeichentest kann man aber auch als parametrischen Test für den Parameter p einer Binomialverteilung auffassen.
Als Beispiel für einen parametrischen Test wird im folgenden der t-Test vorgestellt. Mit diesem Test werden Hypothesen über den Erwartungswert einer Normalverteilung geprüft. Es gibt ihn als Einstichproben- und als Zweistichprobentest für verbundene und unverbundene Stichproben. Der Zweistichproben-t-Test für verbundene Stichproben ist rechnerisch identisch mit dem Einstichproben-t-Test angewandt auf die Differenzen aus den verbundenen Stichproben.
In einer Klinik soll geprüft werden, ob der Erwartungswert der Geburtsgewichte von Neugeborenen nach unauffälliger Schwangerschaft dem Bundesdurchschnitt von µ0 = 3200 g entspricht.
Es wird vorausgesetzt, dass das Geburtsgewicht normalverteilt ist, Voraussetzungen über die Standardabweichung werden nicht gemacht.
Die Nullhypothese H0 und die zweiseitige Alternativhypothese H1 lauten:
H0: µ = 3200 g ( = µ0 )
H1: µ3200 g
Die Irrtumswahrscheinlichkeit sei
= 0.05. Zur Prüfung der Hypothese betrachten wir die Stichprobe vom Umfang n = 20 aus Tabelle 7.3 mit
Die Berechnung der Prüfgröße erfolgt nach der folgenden Formel:
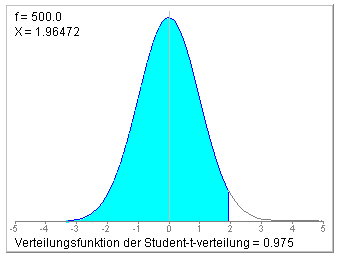
Diese Prüfgröße muss mit dem Quantil t19;0.975 verglichen werden.
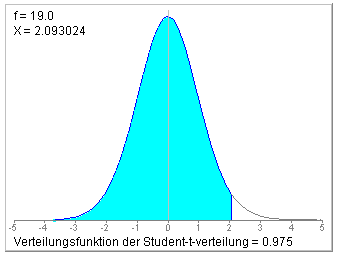
Man findet t19;0.975=2.093. Da die Prüfgröße größer ist als das Quantil, lautet die Testentscheidung: H0 verwerfen. Zur gleichen Entscheidung kommt man, wenn man für den berechneten t-Wert die zweiseitige Überschreitungswahrscheinlichkeit berechnet. Für das obige Beispiel ergibt sich ein p-Wert von 0.0319 und damit ein Wert unter der vorgegebenen Irrtumswahrscheinlichkeit von 0.05.
Fehler 2. Art nicht in Betracht.
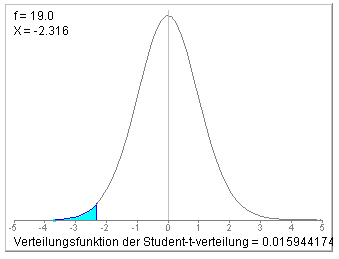
Da H0 verworfen wurde, kommt der
Es lässt sich mathematisch zeigen, dass das Konfidenzintervall genau die Werte enthält, für die die Nullhypothese nicht verworfen wird. µ0 = 3200 liegt nicht in dem in Tabelle 7.4 berechneten Konfidenzintervall [3227.9,3752.1].Tabelle 8.1: Hämoglobinwerte vor und nach der Behandlung
Hämoglobinwerte
Pat.-Nr.
vorher
nachher
Differenz (vorher - nachher)
1
11.2
9.9
1.3
2
9.4
10.8
-1.4
3
9.9
10.3
-0.4
4
9.3
9.9
-0.6
5
8.9
7.5
1.4
6
8.2
8.9
-0.7
7
10.5
10.4
0.1
8
8.8
8.5
0.3
9
10.3
8.2
2.1
10
9.8
10.1
-0.3
Mittelwert 9.63
9.45
0.18
Standard- abweichung
0.8945
1.0977
1.1003
In Kapitel 6 wurde bereits mit dem Vorzeichen- und mit dem Wilcoxontest geprüft, ob die Hämoglobinwerte durch die Behandlung beeinflusst werden.
Wir prüfen mit dem t-Test für verbundene Stichproben, ob die Behandlung den Hämoglobinwert beeinflusst.
Beim t-Test für verbundene Stichproben benötigt man die Voraussetzung, dass die Differenzen ( hier: Hbvorher -Hbnachher ) normalverteilt sind.
Die Null- und Alternativhypothese für die zweiseitige Fragestellung in der für den t-Test angemessenen Form lautet:
H0: µd = 0
H1: µdWir wählen wieder
Diese Prüfgröße muss mit dem Quantil t9;0.975 verglichen werden bzw. der zugehörige p-Wert mit der Irrtumswahrscheinlichkeit. Man findet t9;0.975=2.26216 bzw. einen p-Wert von 0.6174.
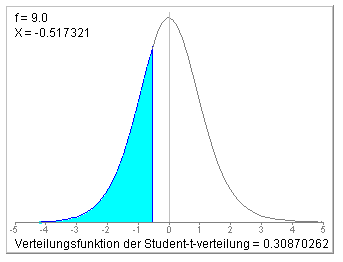
Da die Prüfgröße nicht größer ist als das Quantil, bzw. der p-Wert größer ist als die Irrtumswahrscheinlichkeit lautet die Testentscheidung: H0 nicht verwerfen. In allen drei Tests konnte die Nullhypothese nicht verworfen werden. Allgemein gilt, dass in Situationen, in denen alle drei Tests zulässig sind, der t-Test schärfer ist als der Wilcoxon-Test und dieser wiederum schärfer als der Vorzeichentest
Es soll mit einem t-Test für unverbundene Stichproben geprüft werden, ob Neugeborene nach unauffälliger Schwangerschaft in einer Klinik A deutlich schwerer sind als entsprechende Neugeborene in Klinik B.
Hierzu werden aus den entsprechenden Kliniken zufällige Stichproben gezogen. Zur Auswertung kommen 27 Geburtsprotokolle aus Klinik A und 25 Geburtsprotokolle aus Klinik B.
Tabelle 8.2 enthält die erforderlichen statistischen Maßzahlen:
Tabelle 8.2: Statistische Maßzahlen für das Merkmal 'Geburtsgewicht'
Stichprobenumfang n arithmetischer Mittelwert empirische Standardabweichung Klinik A 27 3785 512 Klinik B 25 3210 530 Voraussetzung für den t-Test für unverbundene Stichproben ist, dass die Daten beider Stichproben Realisationen unabhängiger normalverteilter Zufallsvariabler sind, die in beiden Stichproben die gleiche Varianz haben.
Die hier betrachteten beiden Stichproben sind unverbunden, weil es sich um zwei verschiedene Personengruppen handelt.
Die Null- und Alternativhypothese für die einseitige Fragestellung in der für diesen t-Test angemessenen Form lautet:
H0: µA <= µB
H1: µA > µB
Hier sind µA bzw. µB die erwarteten Geburtsgewichte in Klinik A bzw. Klinik B.Wir wählen wieder
Diese Prüfgröße muss mit dem Quantil t50;0.95 verglichen werden. Man findet:
t50;0.95 = 1.676 bzw. einen einseitigen p-Wert von 0.0001
Da die Prüfgröße größer ist als das Quantil, bzw. der p-Wert kleiner ist als die Irrtumswahrscheinlichkeit, lautet die Testentscheidung: H0 verwerfen.
Applet zum unverbundenen t-Test
8.4 Mann-Whitney-Wilcoxon-Test (U-Test)
Der Mann-Whitney-Wilcoxon-Test ist ein nichtparametrischer Zweistichprobentest für unverbundene Stichproben und stetige Merkmale. In den zugehörigen beiden Grundgesamtheiten soll die Verteilung des betrachteten Merkmals die gleiche Varianz haben. Unter diesen Voraussetzungen prüft der Mann-Whitney-Wilcoxon-Test, ob die beiden Verteilungen auch bezüglich der Lage übereinstimmen.
Zur Berechnung der Prüfgröße ordnet man die Daten aus beiden Stichproben in einer Rangliste und berechnet die Summe der Rangzahlen der Stichprobe mit dem kleineren Stichprobenumfang. Bei gleichgroßen Stichproben nimmt man eine beliebige der beiden Rangsummen und vergleicht sie mit den Quantilen wn1 und wn2. Bei zweiseitiger Fragestellung gilt: Liegt die Prüfgröße in dem Intervall
,
kann die Nullhypothese nicht verworfen werden, liegt die Prüfgröße nicht in dem Intervall, wird sie mit der Irrtumswahrscheinlichkeit
Die Prüfgröße des Mann-Whitney-Wilcoxon-Tests wird oft unterschiedlich definiert. Bei Benutzung einer Tabelle muss man daher sehr genau darauf achten, dass man eine Quantiltabelle benutzt, die zu der angewandten Definition der Prüfgröße passt.
Tabelle 8.3 enthält die Geburtsgewichte zweier zufälliger Stichproben von 9 (10) Neugeborenen aus Klinik A (Klinik B). Es soll mit dem Mann-Whitney-Wilcoxon-Test geprüft werden, ob sich die Verteilung der Geburtsgewichte in Klinik A von der in Klinik B bezüglich der Lage unterscheidet.
Tabelle 8.3: Geburtsgewichte in Klinik A und Klinik B in g
Nr. Klinik A
Geburtsgewicht Rangzahl
Klinik B Geburtsgewicht Rangzahl
xi r1i yi r2i 1 3050 4 3500 13.5 2 2900 2 3350 10 3 3110 6 3620 15 4 3150 8 3700 17 5 3500 13.5 3130 7 6 3100 5 3830 18 7 2800 1 3850 19 8 3450 12 3260 9 9 2950 3 3680 16 10 3420 11 Summe ------ R1=54.5 ------ R2=135.5
Null- und Alternativhypothese für den Mann-Whitney-Wilcoxon-Test bei zweiseitiger Fragestellung lauten:
H0: Die Geburtsgewichte unterscheiden sich nicht ( FA=FB ).
H1: Die Geburtsgewichte unterscheiden sich ( FA(x+)=FB(x),
Hier sind FA und FB die Verteilungsfunktionen der Geburtsgewichte in den jeweiligen Grundgesamtheiten.
Die Prüfgröße ist w=R1=54.5.
Man muss die Prüfgröße mit den Quantilen w9,10;0.975=114 und w9,10,0.025=66 vergleichen.
Da die Prüfgröße nicht in dem Intervall [ 66, 114 ] liegt, muss die Nullhypothese verworfen werden.
8.5 Chi-Quadrat-Test (
2-Test) auf Unabhängigkeit
Tabelle 8.4: Allgemeine Vierfeldertafel
Spalte 1 Spalte 2 Zeilensumme Zeile 1 n11 n12 n1. Zeile 2 n21 n22 n2. Spaltensumme n.1 n.2 n Tabelle 8.5: Therapie und Therapieerfolg bei 140 Patienten einer Klinischen Studie
Therapie CR keine CR Zeilensumme TAD-TAD
Zeilenprozent48
65.8 %25
34.2 %73
100 %TAD-HAM
Zeilenprozent47
70.1 %20
29.9 %67
100 %Spaltensumme
Zeilenprozent95
67.9 %45
32.1 %140
100 %Mit dem
Für die allgemeine Vierfeldertafel (Tabelle 8.4) lautet die Prüfgröße des Tests
oder - mit Stetigkeitskorrektur nach Yates -
.
Die Stetigkeitskorrektur sollte für kleine n (etwa n
30) angewandt werden.
Java-Script zum Chi-Quadrat-Test
Tabelle 3.3 aus Kapitel 3 enthält die Daten über Therapie und Therapieergebnis bei 140 Patienten einer randomisierten Klinischen Studie. Die Therapie war erfolgreich, wenn die Patienten eine vollständige Remission (engl.: complete remission = CR) erreichten. Wenn man die Daten der Tabelle 3.3 auf Erfolg (= CR) und Misserfolg (= keine CR) reduziert, erhält man die Vierfeldertafel in Tabelle 8.5.
Wir prüfen anhand der Daten aus Tabelle 8.5 mit dem Chi-Quadrat-Test, ob die Erfolgsaussichten der beiden Therapien unterschiedlich sind.
Null- und Alternativhypothese für den Chi-Quadrat-Test lauten:
H0: Beide Therapien bieten gleiche Erfolgsaussichten (p1=p2 ).
H1: Beide Therapien bieten ungleiche Erfolgsaussichten ( p1
Hier sind p1 bzw. p2 die Erfolgswahrscheinlichkeiten unter TAD-TAD bzw. TAD-HAM.
Als Signifikanzniveau - d. h. obere Grenze für die Irrtumswahrscheinlichkeit für den Fehler 1. Art - wird
Die Prüfgröße ist
Bei dem Stichprobenumfang n=140 ist die Stetigkeitskorrektur nicht erforderlich.
Die Teststatistik folgt einer Chi-Quadrat-Verteilung mit k=1 Freiheitsgrad.
Daher muss die Prüfgröße mit dem Quantil
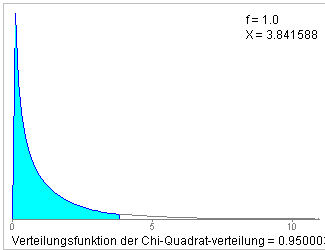
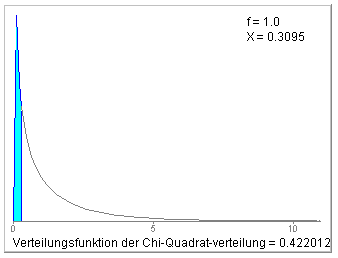
Da die Prüfgröße nicht größer ist als das Quantil, bzw. die Überschreitungswahrscheinlichkeit von 0.578 größer als die vorgegebene Irrtumswahrscheinlichkeit ist, kann die Nullhypothese nicht verworfen werden. Die Daten lassen keinen Widerspruch zur Hypothese gleicher Erfolgsaussichten erkennen.
8.6 Logrank-Test
Der Logrank-Test ist ein nichtparametrischer Test zum Vergleich von Überlebensraten in zwei oder mehr unverbundenen Stichproben. Hier wird nur der Fall zweier Stichproben betrachtet. Bei dem Test wird vorausgesetzt, dass die beiden zu vergleichenden Überlebensraten S1(t) und S2(t) in der Beziehung
S2(t) = S1(t)c, c>0,
stehen, und es wird getestet, ob c
In Tabelle 8.6 sind die aufsteigend sortierten Remissionsdauern von 38 Patienten aus zwei Therapien A und B angegeben. Der mit "Status" überschriebenen Spalte entnimmt man, ob die Remission noch anhält ("in Rem.") oder ob ein Rezidiv eingetreten ist. Anhaltende Remissionen sind sogenannte zensierte Überlebenszeiten. Abbildung 8.1 enthält die zugehörigen Kaplan-Meier-Schätzungen. Zur Berechnung der Prüfgröße des Logrank-Tests muss man die theoretisch zu erwartenden Rezidive ermitteln, wobei man annimmt, dass für beide Gruppen das gleiche Rezidivrisiko besteht (Nullhypothese).
Zum Zeitpunkt t1 = 30 ist das erste Rezidiv aufgetreten. Diesen Zeitpunkt haben alle 38 Patienten erreicht, 20 in Gruppe A und 18 in Gruppe B. Unter der Annahme gleichen Risikos erwartet man das Rezidiv mit Wahrscheinlichkeit 20/38 = 0.5263 in Gruppe A bzw. mit Wahrscheinlichkeit 18/38 = 0.4737 in Gruppe B. Tatsächlich ist es in Gruppe B eingetreten. Auf diese Weise werden die Angaben in den Spalten "erwartete Rezidive" errechnet. Durch Aufsummieren erhält man die erwarteten Anzahlen an Rezidiven EA und EB in den beiden Therapiegruppen. Diese werden den tatsächlich beobachteten Anzahlen BA und BB gegenübergestellt, und man erhält mit
die Prüfgröße des Logrank-Tests. Ist sie größer als das der gewählten Irrtumswahrscheinlichkeit entsprechende Quantil der
Die hier angegebene Prüfgröße ist eine konservative Version des Logrank-Tests. Manche Statistiksysteme geben eine etwas schärfere Version an, die aber aufwendiger zu berechnen ist.
Abbildung 8.1: Kaplan-Meier-Schätzung
Anhand der Daten aus Tabelle 8.6 wird mit dem Logrank-Test überprüft, ob die Remissionsdauern in den beiden Therapiegruppen der gleichen Verteilung folgen. Die Wahrscheinlichkeit für den Fehler 1. Art sei
Null- und Alternativhypothese für den Logrank-Test lauten:
H0: Die Remissionsdauern folgen in beiden Therapiearmen der gleichen Verteilung ( SB=ScA , c=1 ).
H1: Die Remissionsdauern in den beiden Therapiearmen folgen nicht der gleichen Verteilung ( c
Die Prüfgröße des Logrank-Tests ist
.
Die Teststatistik folgt hier - beim Vergleich zweier Therapiearme - einer
Da die Prüfgröße kleiner ist als das Quantil, bzw. die Überschreitungswahrscheinlichkeit von 0.092 größer als die vorgegebene Irrtumswahrscheinlichkeit ist, kann die Nullhypothese nicht verworfen werden. Die Daten lassen - noch ? - keinen Widerspruch zu der Hypothese erkennen, dass die Remissionsdauern unter beiden Therapien der gleichen Verteilung folgen.
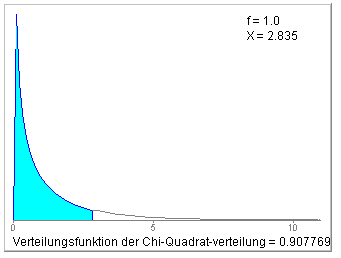
Tabelle 8.6: Remissionsdauern von 38 Patienten aus zwei Therapiegruppen
Remissionsdauer (Tage)
Status
Therapie
Rezidive
in A / in Bim Risiko
gesamt / in A / in BErwartete Rezidive
in A / in B30
Rezidiv
B
0
1
38
20
18
0.5263
0.4737
88
Rezidiv
B
0
1
37
20
17
0.5405
0.4595
100
Rezidiv
B
0
1
36
20
16
0.5556
0.4444
108
Rezidiv
A
1
0
35
20
15
0.5714
0.4286
233
Rezidiv
B
0
1
34
19
15
0.5588
0.4412
262
Rezidiv
A
1
0
33
19
14
0.5758
0.4242
376
in Rem.
B
0
0
32
18
14
0.0000
0.0000
423
in Rem.
A
0
0
31
18
13
0.0000
0.0000
436
in Rem.
A
0
0
30
17
13
0.0000
0.0000
501
Rezidiv
A
1
0
29
16
13
0.5517
0.4483
520
Rezidiv
B
0
1
28
15
13
0.5357
0.4643
559
in Rem.
A
0
0
27
15
12
0.0000
0.0000
573
in Rem.
B
0
0
26
14
12
0.0000
0.0000
582
Rezidiv
A
1
0
25
14
11
0.5600
0.4400
735
in Rem.
B
0
0
24
13
11
0.0000
0.0000
739
in Rem.
B
0
0
23
13
10
0.0000
0.0000
749
in Rem.
B
0
0
22
13
9
0.0000
0.0000
786
Rezidiv
B
0
1
21
13
8
0.6190
0.3810
787
in Rem.
B
0
0
20
13
7
0.0000
0.0000
802
in Rem.
B
0
0
19
13
6
0.0000
0.0000
807
in Rem.
B
0
0
18
13
5
0.0000
0.0000
820
Rezidiv
B
0
1
17
13
4
0.7647
0.2353
824
Rezidiv
A
1
0
16
13
3
0.8125
0.1875
878
Rezidiv
B
0
1
15
12
3
0.8000
0.2000
883
Rezidiv
A
1
0
14
12
2
0.8571
0.1429
932
in Rem.
A
0
0
13
11
2
0.0000
0.0000
960
Rezidiv
A
1
0
12
10
2
0.8333
0.1667
960
in Rem.
A
0
0
11
9
2
0.0000
0.0000
972
Rezidiv
A
1
0
10
8
2
0.8000
0.2000
972
in Rem.
A
0
0
9
7
2
0.0000
0.0000
997
in Rem.
B
0
0
8
6
2
0.0000
0.0000
1013
Rezidiv
B
0
1
7
6
1
0.8571
0.1429
1146
in Rem.
A
0
0
6
6
0
0.0000
0.0000
1147
in Rem.
A
0
0
5
5
0
0.0000
0.0000
1186
in Rem.
A
0
0
4
4
0
0.0000
0.0000
1200
Rezidiv
A
1
0
3
3
0
1.0000
0.0000
1220
in Rem.
A
0
0
2
2
0
0.0000
0.0000
1487
in Rem.
A
0
0
1
1
0
0.0000
0.0000
Summe
--
--
9
9
--
--
--
12.3197
5.6803
Applet-Quantile und Wahrscheinlichkeiten von Verteilungen
Applet-t-Verteilung- Quantile und Wahrscheinlichkeiten
Vierfeldertafel - Chi-Quadrat-Test (Javascript)
Javascript - t-Test für verbundene Stichproben
Applet - t-Test für verbundene Stichproben
Javascript - t-Test für unverbundene Stichproben
Applet - t-Test für unverbundene Stichproben
Javascript - Mann-Whitney-Wilcoxon-Test für unverbundene Stichproben
Applet-Statistischer Test - Power und Fallzahl
