7 Normalverteilung und t-Verteilung
- Verteilungsfunktion und Dichtefunktion der Normalverteilung
- Standardnormalverteilung
- Standardisierung
- Quantile der Normalverteilung
- Zentraler Grenzwertsatz
- Konfidenzintervalle
- t-Verteilung
7.2 Verteilungsfunktion und Dichte
Eine stetige Zufallsvariable X heißt mit Erwartungswert µ
und Varianz ![]() 2 normalverteilt, wenn die Wahrscheinlichkeit dafür, dass X
höchstens gleich x ist, durch das Integral der
Gaußschen Fehlerfunktion gegeben ist, in Formeln:
2 normalverteilt, wenn die Wahrscheinlichkeit dafür, dass X
höchstens gleich x ist, durch das Integral der
Gaußschen Fehlerfunktion gegeben ist, in Formeln:
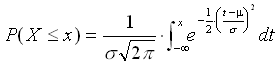 .
.
Hierfür schreibt man abkürzend X:N(µ,![]() 2).
F(x)=P(X
2).
F(x)=P(X![]() x) ist die Verteilungsfunktion der
Normalverteilung. Deren erste Ableitung
x) ist die Verteilungsfunktion der
Normalverteilung. Deren erste Ableitung
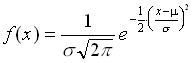
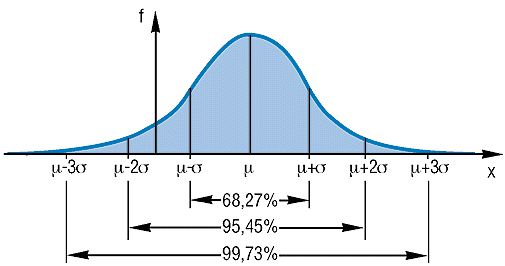
ist die Dichtefunktion der Normalverteilung. Das Bild der Dichtefunktion ist die bekannte Glockenkurve (Abbildung 7.1):
Abbildung 7.1: Dichtefunktion der
Normalverteilung N(µ,![]() 2)
2)
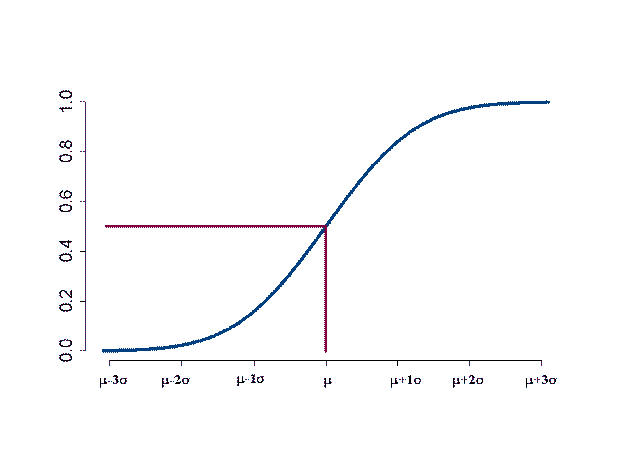
Die Verteilungsfunktion der Normalverteilung hat einen sigmoiden (s-förmigen) Kurvenverlauf (Abbildung 7.2).
Abbildung 7.2: Verteilungsfunktion der
Normalverteilung N(µ,![]() 2)
2)
Es gibt die
Normalverteilung für jedes µ und jedes positive ![]() .
.
Aus den Formeln und den Abbildungen werden die folgenden Eigenschaften der Normalverteilung deutlich:
- Die Dichtefunktion ist symmetrisch um den Erwartungswert µ.
- Sie hat zwei Wendepunkte bei x = µ-
und x = µ+
.
- Sie erreicht ihr Maximum an der Stelle x = µ.
- Der Erwartungswert und der Median stimmen überein.
- Die Dichtefunktion f(x) ist für jede reelle Zahl definiert und immer größer als 0. Für x -> ±
nähert sie sich asymptotisch der x-Achse.
 Dichte- und Verteilungsfunktion-Applet
Normalverteilung
Dichte- und Verteilungsfunktion-Applet
Normalverteilung
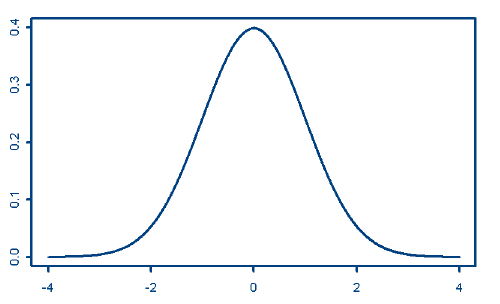
N(0,1), die Normalverteilung mit Erwartungswert 0 und Varianz 1, nennt man Standardnormalverteilung.
Abbildung 7.3: Dichtefunktion der Standardnormalverteilung N(0,1)
Mit der Standardisierungsformel
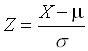
transformiert man eine normalverteilte Zufallsvariable X:N(m,s2) in eine Standardnormalverteilung.
Die Verteilungsfunktion der Standardnormalverteilung wird allgemein mit F bezeichnet. Mit Hilfe einer Tabelle von F, wie sie in vielen Lehrbüchern abgedruckt ist (siehe Tabelle 1 des Tabellenanhangs), kann man den Wert der Verteilungsfunktion F jeder beliebigen Normalverteilung über die Formel
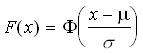
berechnen. Die Quantile zp der Standardnormalverteilung bzw. xp einer beliebigen Normalverteilung kann man mit Hilfe der Formeln
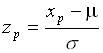 bzw.
bzw. ![]()
umrechnen.
Die Javascript-Prozeduren in diesem Kapitel erlauben die direkte Berechnung aller gewüschten Kenngrößen
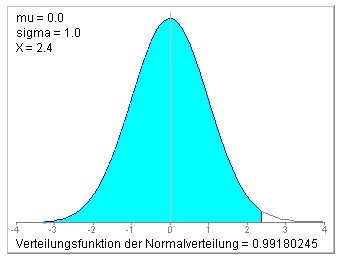
 Applet zur Standardisierung der
Normalverteilung
Applet zur Standardisierung der
Normalverteilung
 Applet zur Berechnung von Quantilen und Wahrscheinlichkeiten für die
Normalverteilung
Applet zur Berechnung von Quantilen und Wahrscheinlichkeiten für die
Normalverteilung
Beispiel 7.1
Das
Geburtsgewicht von Neugeborenen nach unauffälliger
Schwangerschaft sei mit Erwartungswert µ = 3500 g und
Standardabweichung
![]() = 500 g normalverteilt.
= 500 g normalverteilt.
Die Wahrscheinlichkeit, dass ein Neugeborenes aus dieser Grundgesamtheit nicht mehr als 4700 g wiegt, ist dann
.
D.h. die Wahrscheinlichkeit ist 0.9918, in der genannten Grundgesamtheit wiegen damit 99.18 % aller Neugeborenen nicht mehr als als 4700 g.
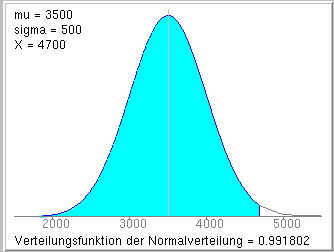
 Berechnung mit dem Applet zur Standardisierung der
Normalverteilung
Berechnung mit dem Applet zur Standardisierung der
Normalverteilung
Es soll eine Grenze für das Geburtsgewicht angegeben werden, die nur vom 2.5 % aller Neugeborenen übertroffen wird.
Es gilt:
D.h. die gesuchte Schranke beträgt 4480 g. In der genannten Grundgesamtheit wiegen also 97.5 % aller Neugeborenen nicht mehr als 4480 g. 2.5 % wiegen mehr als 4480 g.
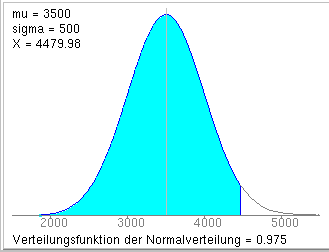
 Berechnung mit einem Applet zur Berechnung von Quantilen einer
Normalverteilung
Berechnung mit einem Applet zur Berechnung von Quantilen einer
Normalverteilung
Die Normalverteilung wird häufig verwendet, um quantitative, symmetrisch verteilte, eingipflige Mermale zu beschreiben. Zum Standardisieren einer Normalverteilung benötigt man deren Erwartungswert und Varianz bzw. Standardabweichung. In der Praxis sind diese häufig nicht bekannt, und man muss sie aus einer Stichprobe durch den arithmetischen Mittelwert und die empirische Varianz bzw. Standardabweichung schätzen. Diese Schätzung aus empirischen Daten ist aber nur dann sinnvoll, wenn es sich um quantitative, symmetrisch verteilte, eingipflige Mermale handelt. Ein erster Hinweis auf Symmetrie liegt dann vor, wenn der Median und der Mittelwert annähernd gleich sind. Eine optische Überprüfung ist durch ein Histogramm mit einer angepassten Normalverteilungsdichte möglich. Die sigmoide Form der empirischen Verteilungsfunktion ist ebenfalls ein Hinweis auf annähernd normalverteilte Merkmale. Noch geeigneter ist der sogenannte Normalverteilungsplot, wo mit Hilfe der Normalverteilung die empirische Verteilungsfunktion so transformiert wird, dass bei normalverteilten Mermalen eine Gerade entsteht. Diese Möglichkeiten veranschaulicht das folgende Beispiel.
Beispiel 7.2
Mit Hilfe des Applets-
 Applet-Exploration und Tests
Applet-Exploration und Tests
Abbildung 7.4: Basisstatistik des Merkmals "Größe"

Median und Mittelwert sind annähernd gleich. Auch das Histogramm zeigt eine gute Übereinstimmung mit der angepassten Normalverteilungsdichte.
Abbildung 7.5: Histogramm mit angepasster Normalverteilungsdichte des Merkmals "Größe"

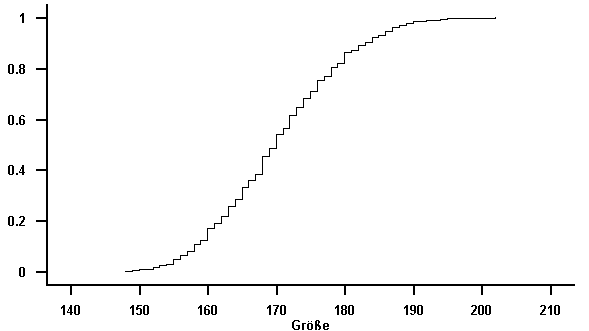
Die empirische Verteilungsfunktion zeigt ebenfalls die für die Normalverteilung typische sigmoide Form.
Abbildung 7.6: Empirische Verteilungsfunktion des Merkmals "Größe"
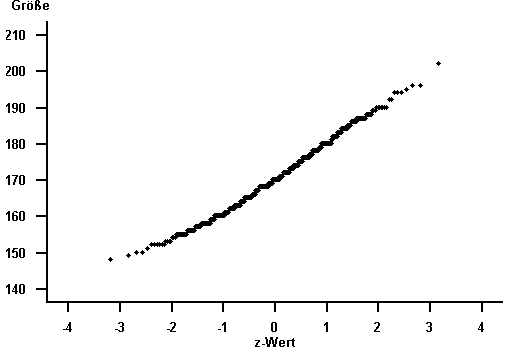
Der Normalverteilungsplot gibt annähernd eine Gerade wieder. Das Merkmal "Größe" kann als normalverteilt mit Erwartungswert 170 cm und Standardabweichung 9.4 cm angenommen werden.
Abbildung 7.7: Normalverteilungsplot des Merkmals "Größe"
Leider sind in der Medizin viele Merkmale nicht normalverteilt sondern rechtsschief verteilt; d.h. die Dichtefunktion ist nicht symmetrisch sondern hat einen Gipfel am linken Rand und einen langen Auslauf an der rechten Seite. Ein erster Hinweis auf Nichtsymmetrie liegt dann vor, wenn der Median und der Mittelwert stark unterschiedlich sind. Eine optische Überprüfung ist durch ein Histogramm mit einer schlecht angepassten Normalverteilungsdichte möglich. Die sigmoide Form der empirischen Verteilungsfunktion liegt bei solchen nichtnormalverteilten Merkmalen nicht vor. Noch geeigneter ist der Normalverteilungsplot, der keine Gerade zeigt. Viele solcher Merkmale folgen einer logarithmischen Normalverteilung, d.h. ihre logarithmierten Werte sind normalverteilt. Durch eine Logarithmustransformation erhält man dann ein normalverteiltes Merkmal. Diese Möglichkeiten veranschaulicht das folgende Beispiel.
Beispiel 7.3
Mit Hilfe des Applets-
 Applet-Exploration und Tests
Applet-Exploration und Tests
Abbildung 7.8: Basisstatistik des Merkmals "LDH und log(LDH)"

Median und Mittelwert unterscheiden sich beim "LDH" stark, sind aber annähernd gleich beim "log(LDH)". Auch das Histogramm zeigt beim "LDH" eine schlechte Übereinstimmung mit der angepassten Normalverteilungsdichte und eine gute Übereinstimmung bei den logarithmierten Werten.
Abbildung 7.9: Histogramm mit angepasster Normalverteilungsdichte des Merkmals "LDH"
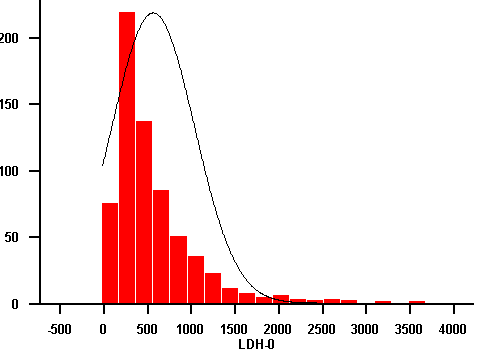
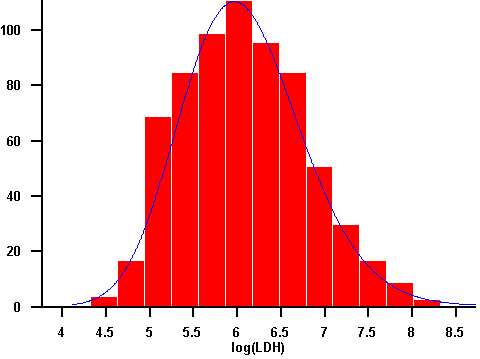
Abbildung 7.10: Histogramm mit angepasster Normalverteilungsdichte des Merkmals "log(LDH)"
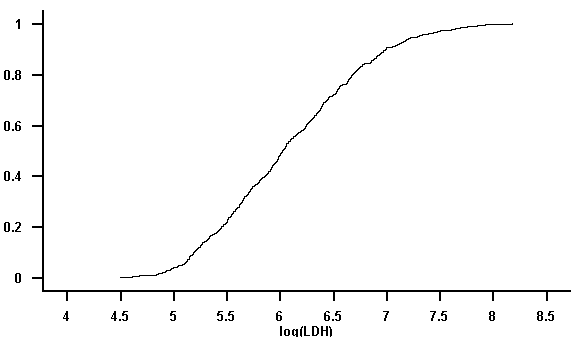
Die empirische Verteilungsfunktion zeigt für das "LDH" ebenfalls nicht die für die Normalverteilung typische sigmoide Form. Beim "log(LDH)" ist diese Form zu sehen.
Abbildung 7.11: Empirische Verteilungsfunktion des Merkmals "LDH"
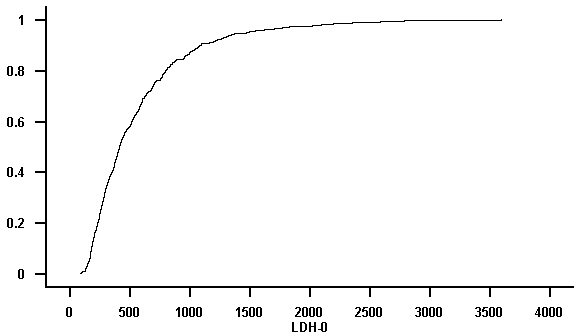
Abbildung 7.12: Empirische Verteilungsfunktion des Merkmals "log(LDH)"
Der Normalverteilungsplot für das "LDH" weicht stark von einer Geraden ab, gibt aber annähernd für das "log(LDH)" eine Gerade wieder.
Abbildung 7.13: Normalverteilungsplot des Merkmals "LDH"
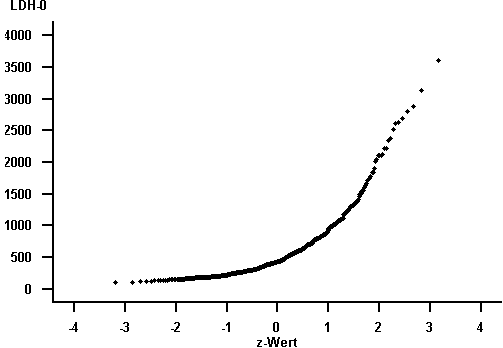
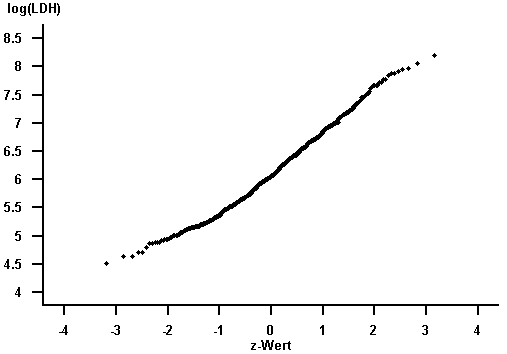
Abbildung 7.14: Normalverteilungsplot des Merkmals "log(LDH)"
Arithmetischer Mittelwert und empirische Standardabweichung sind die Schätzwerte für die Standardisierung. Die Subtraktion des Mittelwertes bei der Standardisierung ist unproblematisch, man erhält eine Normalverteilung mit Erwartungswert 0. Beim Dividieren durch die empirische Standardabweichung ergibt sich aber das Problem, dass die Verteilung des Quotienten keine Normalverteilung mehr ist. W. Gosset hat 1903 die resultierende Verteilung berechnet und ihr den Namen t-Verteilung gegeben. Er hat gezeigt, dass ihre Dichtefunktion der Gleichung
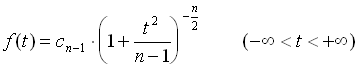
genügt. Hierin ist cn-1 eine Konstante, die sich aus der Gleichung
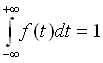
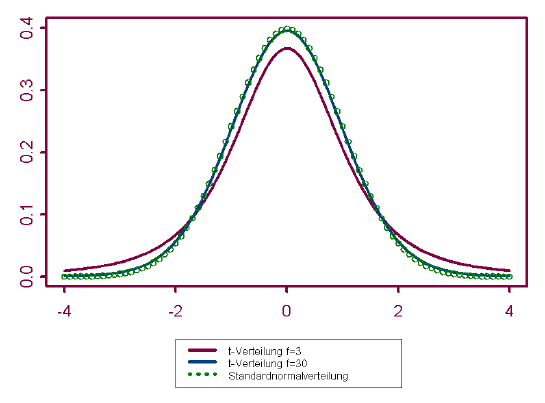
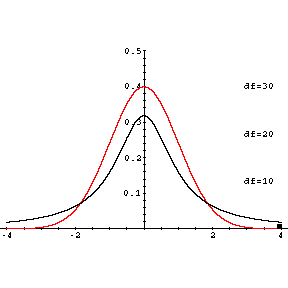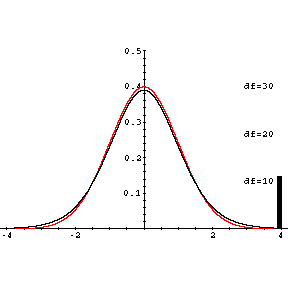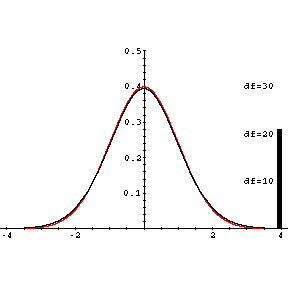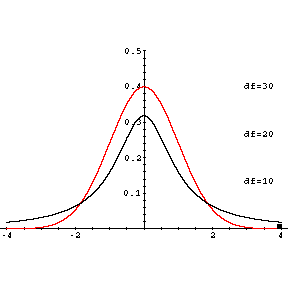
bestimmen lässt. Der Graph von f ähnelt dem der Dichte der Standardnormalverteilung. f hat sein Maximum bei t=0 und nähert sich symmetrisch zur y-Achse asymptotisch der t-Achse. Die Form der Verteilung hängt noch vom Umfang n der Stichprobe ab, aus der die empirische Standardabweichung berechnet wurde. Je größer n ist, desto mehr nähert sich die t-Verteilung der Standardnormalverteilung an.
Historisch hat es sich eingebürgert, die verschiedenen t-Verteilungen nicht mit n sondern mit f=n-1, der sogenannten Zahl der Freiheitsgrade (engl. degrees of freedom (df)) durchzunumerieren.
Abbildung 7.15: Dichtefunktion der t-Verteilung (f=3 und f=30) und der Standardnormalverteilung
 Applet - Dichtefunktion der t-Verteilung und der Normalverteilung
Applet - Dichtefunktion der t-Verteilung und der Normalverteilung
Die t-Verteilung braucht man insbesondere dann, wenn man Hypothesen über den Erwartungswert einer Normalverteilung prüfen will, deren Standardabweichung nicht bekannt ist (t-Test, Kapitel 8).
Übungsaufgabe 7.1
Eine Klinikapotheke benötigt täglich
im Durchschnitt etwa 1000 g einer bestimmten Substanz X.
Angenommen, der tägliche Verbrauch sei mit
Erwartungswert µ = 1000 g und Standardabweichung ![]() = 200 g
normalverteilt.
= 200 g
normalverteilt.
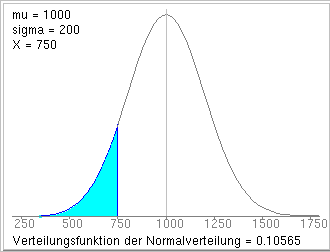
Wie groß ist die Wahrscheinlichkeit, dass an einem Tag weniger als 750 g benötigt werden ?
Wie groß ist die Wahrscheinlichkeit, dass der Bedarf an einem Tag
a) zwischen 800 und 1200 g
b) zwischen 600 und 1400 g
c) zwischen 400 und 1600 g
liegt?
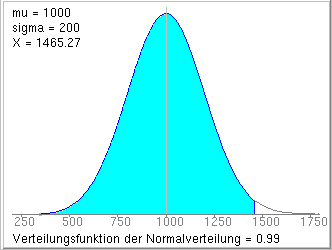
Wie groß muss der Vorrat der Apotheke mindestens sein, damit der tägliche Bedarf ohne Nachbestellung mit 99 % (99.9 %) Sicherheit gedeckt werden kann?
Der zentrale Grenzwertsatz besagt, dass die Summe unabhängiger Zufallsvariablen, die alle die gleiche Verteilungsfunktion besitzen, näherungsweise normalverteilt ist. Die Annäherung ist umso besser, je größer die Anzahl der Summanden ist.
Eine binomialverteilte Zufallsvariable X ist z.B. eine Summe von n unabhängigen bernoulliverteilten Zufallsvariablen Y1,Y2,Y3,...,Yn:
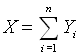 .
.
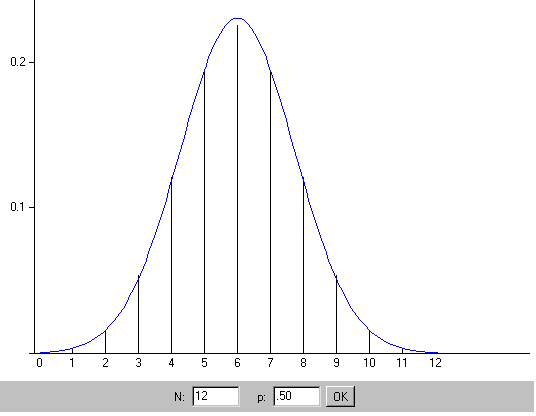
Nach dem Zentralen Grenzwertsatz lässt sich die Binomialverteilung mit dem Erwartungswert np und der Varianz np(1-p) näherungsweise durch die entsprechende Normalverteilung mit dem Erwartungswert np und der Varianz np(1-p) ersetzen.
Abbildung 7.16: Anpassung der Binomialverteilung durch die Normalverteilung
 Applet zur Approximation der Binomialverteilung durch die Normalverteilung
Applet zur Approximation der Binomialverteilung durch die Normalverteilung
An einer Skizze kann man sich klarmachen, dass man die Wahrscheinlichkeit
![]()
der Binomialverteilung nicht durch F(k2)-F(k1-1) der entsprechenden Normalverteilung, sondern besser durch F(k2+½)-F(k1-½) approximiert. Diese Korrektur nennt man Stetigkeitskorrektur.
Beispiel 7.4
In einer Grundgesamtheit haben 40 % aller Personen die Blutgruppe 0. Wie groß ist die Wahrscheinlichkeit, dass in einer zufälligen Stichprobe vom Umfang n=10, 50, 100 aus dieser Grundgesamtheit der Anteil der Personen mit Blutgruppe 0 zwischen 30 % und 50 % liegt? Die folgende Tabelle enthält die gefragten Wahrscheinlichkeiten sowohl über die Binomialverteilung als auch näherungsweise über die entsprechende Normalverteilung mit und ohne Stetigkeitskorrektur. zu berechnen.
Tabelle 7.1: Approximation der Binomialverteilung durch die Normalverteilung
| n | Binomialverteilung | Normalverteilung | Normalverteilung (korrigiert) |
| 10 | 0.66647 | 0.64234 | 0.66708 |
| 50 | 0.88870 | 0.88391 | 0.88765 |
| 100 | 0.96846 | 0.96701 | 0.96791 |
Der unbekannte Erwartungswert µ einer
Normalverteilung N(
µ,![]() 2)
wird durch den Mittelwert
2)
wird durch den Mittelwert ![]() aus einer
zufälligen Stichprobe geschätzt. Zu dem Mittelwert
lässt sich ein Intervall, das sogenannte Konfidenzintervall, angeben, das den unbekannten Erwartungswert µ
mit einer vorgegebenen Konfidenzwahrscheinlichkeit 1-
aus einer
zufälligen Stichprobe geschätzt. Zu dem Mittelwert
lässt sich ein Intervall, das sogenannte Konfidenzintervall, angeben, das den unbekannten Erwartungswert µ
mit einer vorgegebenen Konfidenzwahrscheinlichkeit 1-![]() enthält.
Die Intervallgrenzen tu bzw.
to berechnet man aus den
Formeln
enthält.
Die Intervallgrenzen tu bzw.
to berechnet man aus den
Formeln
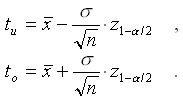
Dabei ist ![]() die Standardabweichung der betrachteten
Normalverteilung. n ist der Stichprobenumfang und z1-a /2 das (1-a
/2)-Quantil der Standardnormalverteilung.
die Standardabweichung der betrachteten
Normalverteilung. n ist der Stichprobenumfang und z1-a /2 das (1-a
/2)-Quantil der Standardnormalverteilung.
Wenn die Standardabweichung ![]() nicht bekannt ist, muss sie ebenfalls aus der Stichprobe
geschätzt werden. Als Schätzwert benutzt man die
empirische Standardabweichung s. In den Formeln
für die Intervallgrenzen muss dann aber auch das Quantil
z1-a
/2 der Standardnormalverteilung durch das
Quantil tn-1;1-a/2 der tn-1-Verteilung
ersetzt werden (vgl. Abschnitt 7.2). Man erhält
nicht bekannt ist, muss sie ebenfalls aus der Stichprobe
geschätzt werden. Als Schätzwert benutzt man die
empirische Standardabweichung s. In den Formeln
für die Intervallgrenzen muss dann aber auch das Quantil
z1-a
/2 der Standardnormalverteilung durch das
Quantil tn-1;1-a/2 der tn-1-Verteilung
ersetzt werden (vgl. Abschnitt 7.2). Man erhält
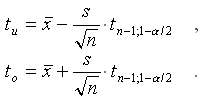
 Applet zur Simulation von Konfidenzintervallen
Applet zur Simulation von Konfidenzintervallen
 Javascript und Applet - Konfidenzintervalle
Javascript und Applet - Konfidenzintervalle
Beispiel 7.3
Es wird vorausgesetzt, dass das Körpergewicht von Neugeborenen nach unauffälliger Schwangerschaft und unter Ausschluss von Mehrlingsgeburten einer Normalverteilung N(µ,
2) folgt.
Geht man von der Standardabweichung
= 500 g aus, und wählt die Konfidenzwahrscheinlichkeit 1-
= 0.95 (d. h. Irrtumswahrscheinlichkeit
= 0.05), dann ergeben sich die in Tabelle 7.2 wiedergegebenen zweiseitigen Konfidenzintervalle für den unbekannten Erwartungswert µ.
Tabelle 7.2: Konfidenzintervall bei gegebener Standardabweichung
| Stichprobenumfang | Mittelwert | untere Grenze |
obere Grenze |
Intervall- länge |
10 |
3620 |
3310.1 |
3929.9 |
619.8 |
20 |
3490 |
3270.9 |
3709.1 |
438.2 |
40 |
3570 |
3415.1 |
3724.9 |
309.8 |
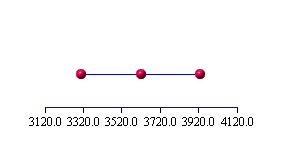
Wird die Standardabweichung wie angegeben aus der Stichprobe geschätzt, so muss man statt der Quantile der Standardnormalverteilung die Quantile der entsprechenden t-Verteilung benutzen und erhält die Ergebnisse in Tabelle 7.3. Die benötigten Quantilwerte der t-Verteilung sind in Tabelle 7.4 enthalten.
Tabelle 7.3: Konfidenzintervall bei empirischer Standardabweichung (
= 0.05)
| Stichprobenumfang | Mittelwert | emp. Standardabw. | untere Grenze | obere Grenze | Intervallänge |
10 |
3620 |
470 |
3283.8 |
3956.2 |
672.4 |
20 |
3490 |
560 |
3752.1 |
524.2 |
|
40 |
3570 |
510 |
3406.9 |
3733.1 |
326.2 |
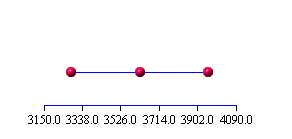
Tabelle 7.4: Ausgewählte Quantile der tf-Verteilung
| f | 9 | 19 | 39 | |
| tf;0.975 | 2.262 | 2.093 | 2.023 | 1.96 |

Applet-Dichte- und Verteilungsfunktion der Normalverteilung
Applet-Standardisierung der Normalverteilung
Applet-Quantile und Wahrscheinlichkeiten von Verteilungen
Applet-Quantile der Normalverteilung
Applet - Histogramm und Normalverteilungsplot
Applet-Dichtefunktion der t-Verteilung und Normalverteilung
Applet-t-Verteilung- Quantile und Wahrscheinlichkeiten
Applet-Approximation der Binomialverteilung durch die Normalverteilung
Applet-Statistischer Test von Erfolgsraten
Javascript und Applet - Konfidenzintervalle
Applet-Zentraler Grenzwertsatz - Würfeln