�bungen zur medizinischen Biometrie
- Fehler 1. und 2. Art
- Nullhypothese, Alternativhypothese
- einseitige und zweiseitige Alternative
- Irrtumswahrscheinlichkeiten
- Spezielle Tests
� Vorzeichentest
� Wilcoxontest
6.2 Grundlagen
Das Prinzip des statistischen Tests wurde schon in Beispiel 5.3 erw�hnt. Eine vorgegebene Annahme (Nullhypothese H0) wird anhand von Daten �berpr�ft. Wenn die Daten "stark" von dem abweichen, was man unter der Nullhypothese erwartet, l�sst man die Nullhypothese fallen.
Im statistischen Test wird dieses plausible Vorgehen formalisiert.
Nachdem die Nullhypothese H0 und die Alternativhypothese H1 so formuliert sind, dass sie sich gegenseitig ausschlie�en und keine dritte M�glichkeit zulassen, ergibt sich das einfache Entscheidungsschema der Tabelle 6.1.
Tabelle 6.1: Entscheidungsschema beim statistischen Test
Test- |
Wirklichkeit |
|
H0 |
richtig |
Fehler 2. Art |
H1 |
Fehler 1. Art |
richtig |
Der Fehler 1. Art ist der Fehler, die Nullhypothese zu verwerfen, obwohl sie richtig ist.
Der Fehler 2. Art ist der Fehler, die Nullhypothese zu behalten, obwohl sie falsch ist.
Die Entscheidung, H0 zu verwerfen oder zu behalten, wird von der Realisation der Zufallsvariablen abh�ngig gemacht, die man als Teststatistik gew�hlt hat. Hierf�r kommt im Prinzip jede Zufallsvariable in Frage, deren Verteilungsfunktion unter der Nullhypothese bekannt ist. Die Realisation der Teststatistik nennt man auch Pr�fgr��e des Tests.
In der Wahl der geeigneten Teststatistik liegt die eigentliche Kunst des Testens. In den folgenden Abschnitten werden mit dem Vorzeichentest und dem Wilcoxontest zwei einfache Beispiele gegeben, die das allgemeine Prinzip erl�utern sollen. Kapitel 8 enth�lt weitere spezielle Tests.
Der Wertebereich der Teststatistik wird in zwei Teilmengen zerlegt, den Verwerfungsbereich und den Annahmebereich. Wenn die Pr�fgr��e in den Verwerfungsbereich f�llt, wird die Nullhypothese verworfen, ansonsten wird sie behalten.
Da die Verteilungsfunktion der
Teststatistik unter der Nullhypothese bekannt ist, kann
man den Verwerfungsbereich so w�hlen, dass unter H0
seine Wahrscheinlichkeit unter einen vorgegebenen Wert 
f�llt. , das
sogenannte Signifikanzniveau des Tests, ist damit die Obergrenze f�r die
Wahrscheinlichkeit, den Fehler 1. Art zu begehen. wird vom
Versuchsleiter vorgegeben. �bliche Werte f�r sind 0.05,
0.01 und 0.001. Welches man w�hlt, h�ngt
von den Konsequenzen ab, die der Fehler 1. Art hat. Der
naheliegende Wunsch, = 0 zu w�hlen, scheitert daran, dass dann � , die
Wahrscheinlichkeit f�r den Fehler 2. Art, gro� wird.
Man �berlegt sich leicht, dass man = 0
erreicht, wenn man die Nullhypothese immer beh�lt. Aber
dann beh�lt man sie auch, wenn sie falsch ist und
erh�lt � = 1.
und � sind die Irrtumswahrscheinlichkeiten des Tests. Es ist im allgemeinen nicht zu erreichen,
dass die Verteilungsfunktion der Teststatistik auch unter
der Alternativhypothese bekannt ist. Daher l�sst sich � nicht
genauso behandeln wie . Man hat f�r � nur die
unbefriedigende Obergrenze
� 
1-
Das hat zur Folge, dass die Entscheidung ‘H0 behalten’ m�glicherweise mit einer gro�en Irrtumswahrscheinlichkeit behaftet ist. Daher interpretiert man diese Entscheidung meist im Sinne eines Unentschiedens und sagt ‘H0 kann nicht verworfen werden’.
Beispiel 6.1
Es wird vermutet, dass eine bestimmte Behandlung einen Einfluss auf den H�moglobinwert eines Patienten hat. Um dies zu �berpr�fen, wird bei einer Stichprobe von 10 Patienten, die sich dieser Behandlung unterziehen m�ssen, der H�moglobinwert unter standardisierten Bedingungen vor und nach der Behandlung bestimmt (Tabelle 6.3).
Die Formulierung von Null- und Alternativhypothese lautet:
H0: Die Behandlung hat keinen Einfluss auf den Hb.
H1: Die Behandlung beeinflusst den Hb.
In Tabelle 6.2 ist die Entscheidungssituation dargestellt.
Tabelle 6.2: Entscheidungssituation beim speziellen Test
Testentscheidung: |
Wirklichkeit:
der H�moglobinwert Hb |
|
| ...wird nicht beeinflusst | richtig | Fehler 2. Art |
| ...wird beeinflusst | Fehler 1. Art | richtig |
Die Entscheidung ist richtig, wenn die Testentscheidung mit der Wirklichkeit �bereinstimmt.
Der Fehler 1. Art bedeutet, dass die Nullhypothese verworfen wird, obwohl sie richtig ist. Der Fehler 2. Art bedeutet, dass die Nullhypothese nicht verworfen wird, obwohl sie falsch ist.
Beim statistischen Test gibt man eine
obere Schranke (z. B. = 0.05) f�r die Wahrscheinlichkeit des Fehlers
1. Art vor und versucht nach dieser Vorgabe die
Wahrscheinlichkeit b f�r den Fehler 2. Art m�glichst klein zu
halten.
Im allgemeinen w�chst die Wahrscheinlichkeit des Fehlers 2. Art, wenn man die des Fehlers 1. Art verkleinert. Die beschriebene Behandlung der
Fehlerwahrscheinlichkeiten hat zur Folge, dass die
Wahrscheinlichkeit f�r den Fehler 1. Art unter
Kontrolle ist ( ), die f�r den Fehler 2. Art
aber nicht. Wenn die Nullhypothese fallen
gelassen werden muss, kann nur der Fehler 1. Art
auftreten. Die Fehlerwahrscheinlichkeit ist unter
Kontrolle. Das Testergebnis darf entsprechend sicher
formuliert werden ( "H0 kann auf dem
vorgegebenen Signifikanzniveau verworfen werden" ). Wenn die Nullhypothese nicht
fallen gelassen werden darf, kann m�glicherweise der
Fehler 2. Art auftreten. Die Fehlerwahrscheinlichkeit
ist nicht unter Kontrolle. Das Testergebnis muss
entsprechend vorsichtig formuliert werden (
"kein Widerspruch zur Nullhypothese" ).
Der Versuchsleiter muss vor der Durchf�hrung des Versuchs entscheiden, wie die Fragestellung als Alternative f�r den statistischen Test formuliert werden soll. Diese Entscheidung erfolgt nicht unter statistischen Gesichtspunkten, sondern aufgrund inhaltlicher �berlegungen.
Zur Behandlung einer bestimmten Erkrankung stehen zwei Medikamente A und B zur Verf�gung, die beide in der Praxis angewandt werden. Im einfachen Fall einer qualitativen Zielgr��e, die nur die Auspr�gungen Erfolg und Misserfolg hat, ist es naheliegend, den Anteil pA der Patienten, die mit Medikament A erfolgreich behandelt werden, mit dem entsprechenden Anteil pB bei Medikament B zu vergleichen.
Hat der Versuchsleiter a priori keine Vorkenntnisse dar�ber, ob pA gr��er, kleiner oder auch gleich pB ist, pr�ft er zweckm��ig die Alternative
H0: pA = pB,
H1: pA
pB,
Man nennt diese Alternative zweiseitig, weil die interessierende Differenz pA - pB der Erfolgswahrscheinlichkeiten unter H1 sowohl positiv als auch negativ sein kann.
Ist aufgrund inhaltlicher �berlegungen von vornherein klar, dass pB mindestens gleich pA ist oder gr��er sein sollte, pr�ft man zweckm��ig die Alternative
H0: pA
pB
H1: pA < pB.
Man nennt diese Alternative einseitig, weil die interessierende Differenz pA - pB der Erfolgswahrscheinlichkeiten unter H1 nur auf einer Seite der m�glichen Werte sein kann.
Statistischer Test - Power und Fallzahl
6.3 Vorzeichentest
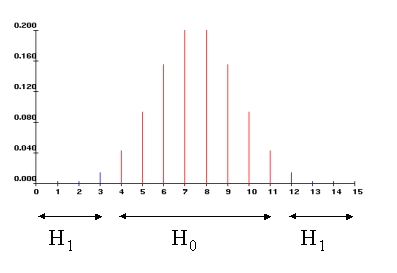
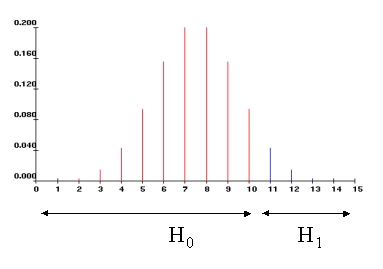
Beim Vorzeichentest geht man bei der zweiseitigen Fragestellung unter H0 davon aus, dass in jedem Einzelfall die Differenz zwischen dem H�moglobinwert vor Therapie und dem nach Therapie jeweils mit der Wahrscheinlichkeit 0.5 entweder positiv oder negativ ist. Die Gleichheit beider Werte h�lt man praktisch f�r ausgeschlossen und ordnet ihr die Wahrscheinlichkeit 0 zu.
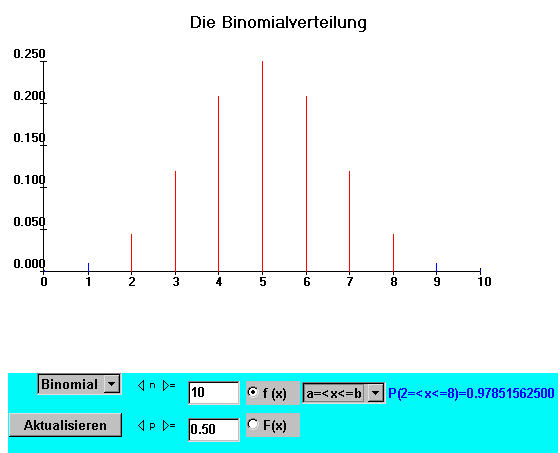
Unter diesen Annahmen folgt die Zufallsvariable D+, die die Anzahl der positiven Differenzen angibt, einer Binomialverteilung mit den Parametern n = ‘Anzahl aller Differenzen’ und p = 0.5, d.h., D+: B(n, 0.5). Damit ist D+ eine Zufallsvariable, deren Verteilung unter der Nullhypothese bekannt ist. Sie l�sst sich daher als Teststatistik einsetzen. D+ ist die Teststatistik des Vorzeichentests (engl.: sign test).
Tabelle 6.3: H�moglobinwerte vor und nach der Behandlung
H�moglobinwerte
Pat.-Nr.
vorher
nachher
Differenz (vorher - nachher)
1
11.2
9.9
1.3
2
9.4
10.8
-1.4
3
9.9
10.3
-0.4
4
9.3
9.9
-0.6
5
8.9
7.5
1.4
6
8.2
8.9
-0.7
7
10.5
10.4
0.1
8
8.8
8.5
0.3
9
10.3
8.2
2.1
10
9.8
10.1
-0.3
Beispiel 6.3
Aus den Differenzen (vorher - nachher) der Tabelle 6.3 ergibt sich die Anzahl d+ der positiven Differenzen:
d+: = 5.
Die Null- und Alternativhypothese als Aussagen �ber p f�r die einseitige bzw. die zweiseitige Fragestellung lauten:
Einseitig:
H0: Der Hb wird durch die Behandlung nicht gesenkt (bzw. nicht angehoben).
H1: Der Hb wird durch die Behandlung gesenkt (bzw. angehoben).Zweiseitig:
H0: Der Hb �ndert sich unter der Behandlung nicht.
H1: Der Hb �ndert sich unter der Behandlung.Als obere Grenze f�r die Irrtumswahrscheinlichkeit f�r den Fehler 1. Art wird
Tabelle 6.4: Wahrscheinlichkeitsfunktion f und Verteilungsfunktion F der Binomialverteilung B(10, 0.5)
x 0
1
2
3
4
5
6
7
8
9
10
f(x) 0.001
0.010
0.044
0.117
0.205
0.246
0.205
0.117
0.044
0.010
0.001
F(x) 0.001
0.011
0.055
0.172
0.377
0.623
0.828
0.945
0.989
0.999
1
Abbildung 6.3: Wahrscheinlichkeitsfunktion der Binomialverteilung B(10,0.5) 
Anhand der Tabelle 6.4, der Abbildung 6.3 und der Javascript-Prozedur erkennt man, dass {d+ >8}={9,10} der Verwerfungsbereich f�r die einseitige und {d+ <2}
{d+ >8} = {0,1,9,10} der Verwerfungsbereich f�r die zweiseitige Fragestellung ist. Im Beispiel mit d+=5 wird die Nullhypothese beibehalten. Dieses Ergebnis wird durch die folgende Javascript-Prozedur noch einmal best�tigt.
Der Vorzeichentest ber�cksichtigt nur das Vorzeichen, nicht aber den Betrag der Differenzen. Daher ist er nicht sehr scharf, d. h. der Unterschied muss schon sehr deutlich sein, damit der Vorzeichentest die Nullhypothese verwirft.
Unter der Sch�rfe g (auch Macht oder G�te, engl.: power) eines Tests versteht man in der Statistik die Wahrscheinlichkeit daf�r, dass der Test die Nullhypothese verwirft, wenn sie wirklich falsch ist, als bedingte Wahrscheinlichkeit geschrieben:
g = P(H0 verwerfen | H0 falsch). Zwischen der Sch�rfe eines Tests g und der Wahrscheinlichkeit f�r den Fehler 2. Art � besteht folgender Zusammenhang : g=1-�.
6.4 Wilcoxontest f�r verbundene Stichproben
Ein Test mit im allgemeinen gr��erer Sch�rfe als der Vorzeichentest ist der Wilcoxontest, der nicht nur das Vorzeichen sondern auch die Gr��e der Differenz zwischen den gemessenen Werten ber�cksichtigt.
Dies geschieht, indem den Absolutbetr�gen der Differenzen Rangzahlen zugeordnet werden. Die kleinste Differenz erh�lt die Rangzahl 1, die gr��te die Rangzahl n . Danach bildet man R+, die Summe der Rangzahlen, die den positiven, und R-, die Summe der Rangzahlen, die den negativen Differenzen zugeordnet wurden. Offenbar gilt:
R++R- = 1+2+3+...+n = n(n+1)/2,
eine Identit�t, die sich zur Rechenkontrolle einsetzen l�sst.
R+ ist die Teststatistik des Wilcoxontests. Die Verteilung von R+ unter der Nullhypothese l�sst sich berechnen. Tabelle 6.6 enth�lt den Teil, den man zur L�sung des Beispiels ben�tigt.
Tabelle 6.5: H�moglobindifferenzen und Rangzahlen
H�moglobin
Rangzahl der
Pat.-Nr.
vorher
nachher
Differenz (vorher-nachher)
Absolutbetr�ge
1
11.2
9.9
1.3
7
2
9.4
10.8
-1.4
8.5
3
9.9
10.3
-0.4
4
4
9.3
9.9
-0.6
5
5
8.9
7.5
1.4
8.5
6
8.2
8.9
-0.7
6
7
10.5
10.4
0.1
1
8
8.8
8.5
0.3
2.5
9
10.3
8.2
2.1
10
10
9.8
10.1
-0.3
2.5
Beispiel 6.4
Aus den Angaben der Tabelle 6.5 berechnet man die Summe r+ der Rangzahlen der positiven und die Summe r- der Rangzahlen der negativen Differenzen:
r+= 29 r-= 26 ,
Rechenkontrolle: r++r- = 29 + 26 = n(n+1)/2 = (10.11)/2 = 55.
r+ ist die Pr�fgr��e des Wilcoxontests.
Die zweiseitige Formulierung lautet:
H0: Der Hb �ndert sich unter der Behandlung nicht.
H1: Der Hb �ndert sich unter der Behandlung.Als obere Grenze f�r die Irrtumswahrscheinlichkeit wird
Anhand der Tabelle 6.6 f�r den Wilcoxontest f�r paarige Stichproben bzw. der folgenden Javascript-Prozedur bilden die Quantile w(10;0.025)=9 und w(10;0.975)=46 die Grenzen des zugeh�rigen Verwerfungsbereichs Die Pr�fgr��e r+=29 liegt innerhalb dieses Intervalls. Daher darf die Nullhypothese nicht verworfen werden.
Tabelle 6.6: Quantile w(n; a ) f�r den Wilcoxontest
n
a
5
6
7
8
9
10
11
12
0.025
--
1
3
4
6
9
11
14
0.975
--
20
25
32
39
46
55
64
0.05
1
3
4
6
9
11
14
18
0.95
14
18
24
30
36
44
52
60
Applet-Binomial- und Poissonverteilung
Javascript und Applet - diskrete Verteilungen
Applet-Statistischer Test - Power und Fallzahl
Applet-Statistischer Test von Erfolgsraten
Javascript - Vorzeichentest f�r verbundene Stichproben
