
Übungen zur medizinischen Biometrie
- diskrete und stetige Zufallsvariable
- Wahrscheinlichkeitsfunktion und Dichtefunktion
- Verteilungsfunktion
- Parameter einer Verteilungsfunktion
· Erwartungswert
· Median
· Varianz
- Binomialverteilung
- Poissonverteilung
5.2 Grundbegriffe
Bei vielen Zufallsexperimenten werden mögliche Ergebnisse oder Ereignisse durch Zahlen beschrieben.
Beispiel 5.1
Bei einem Wurf mit einem Würfel kann man die möglichen Ereignisse 'k geworfene Augen' einfacher durch die Zahl k (k=1,2,...,6) beschreiben.

Dies ist aber nur sinnvoll, wenn - wie in diesem Beispiel - jedem möglichen Ergebnis der Grundmenge eine Zahl zugeordnet wird und die Zuordnung eindeutig ist. Die Zuordnungs- oder Abbildungsvorschrift heißt Zufallsvariable. Der Begriff der Zufallsvariable entspricht dem Begriff des Merkmals in der deskriptiven Statistik. In diesem Kapitel wird dargelegt, wie eine Merkmalsverteilung mittels mathematischer Funktionen und statistischer Kenngrößen beschrieben werden kann. Wie bei den quantitativen Merkmalen unterscheiden wir diskrete und stetige Zufallsvariable.
Diskrete Zufallsvariable:
Der Wertebereich der Zufallsvariablen besteht aus diskret
auf der Zahlengeraden liegenden Zahlen x1,x2,...(vgl.:
quantitativ diskretes Merkmal).
Beispiel 5.1 (Fortsetzung)
Bei der Zufallsvariablen 'gewürfelte Augenzahl' besteht der Wertebereich aus den Zahlen 1,2,3,4,5,6.
Wahrscheinlichkeitsfunktion f:
f ( xj ) = pj = P ( X=xj ) (j=1,2,...) . (5.1)
Die Wahrscheinlichkeitsfunktion f liefert zu jedem x die Wahrscheinlichkeit, mit der die Zufallsvariable X den Wert x annimmt. Sie ist das theoretische Analogon zur Häufigkeitsverteilung eines diskreten Merkmals in der deskriptiven Statistik.
Beispiel 5.1 (Fortsetzung)
Bei der Zufallsvariablen 'gewürfelte Augenzahl' gilt für die Wahrscheinlichkeitsfunktion f ( xj ) = 1/6 (j=1,2,3,4,5,6).
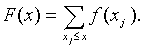 (5.2)
(5.2)
Die Verteilungsfunktion F liefert zu jedem x die Wahrscheinlichkeit, mit der die Zufallsvariable X Werte kleiner oder gleich x annimmt. Sie ist das theoretische Analogon zur empirischen Verteilungsfunktion in der deskriptiven Statistik.
Beispiel 5.1 (Fortsetzung)
Für die Zufallsvariablen 'gewürfelte Augenzahl' ergibt sich die in Abbildung 5.2 dargestellte Verteilungsfunktion F ( x ) .
Erwartungswert E(X):
![]() (5.3)
(5.3)
Der Erwartungswert E(X) einer Zufallsvariablen X ist formal ähnlich gebildet wie der arithmetische Mittelwert, nur sind die beim Mittelwert auftretenden relativen Häufigkeiten durch Wahrscheinlichkeiten ersetzt. Aus dem Gesetz der großen Zahl folgt daher, dass sich mit wachsendem Stichprobenumfang n der arithmetische Mittelwert immer mehr dem Erwartungswert nähert.
Beispiel 5.1 (Fortsetzung)
Bei der Zufallsvariablen 'gewürfelte Augenzahl' gilt für den Erwartungswert E ( X ) = 1*1/6 + 2*1/6 + 3*1/6 + 4*1/6 + 5*1/6 + 6*1/6 = 21/6 = 3.5 .
Varianz V(X):
![]() (5.4)
(5.4)
Die Varianz V(X) einer
Zufallsvariablen ist die erwartete quadratische
Abweichung der Zufallsvariablen X von ihrem
Erwartungswert E(X). Sie ist das theoretische
Analogon zur empirischen Varianz der deskriptiven
Statistik. Die positive Wurzel ![]() aus der Varianz
heißt Standardabweichung.
aus der Varianz
heißt Standardabweichung.
Beispiel 5.1 (Fortsetzung)
Bei der Zufallsvariablen 'gewürfelte Augenzahl' gilt für die Varianz V ( X ) = (1-3.5)2*1/6 + (2-3.5)2*1/6 + (3-3.5)2*1/6 + (4-3.5)2*1/6 + (5-3.5)2*1/6 + (6-3.5)2*1/6 = 17.5/6 = 2.91667 .
Stetige Zufallsvariable:
Der Wertebereich einer stetigen Zufallsvariablen umfasst ein ganzes
Intervall der Zahlengeraden (vgl.: quantitativ stetiges
Merkmal).
Bei der Verteilungsfunktion F(x) einer stetigen Zufallsvariable wird das Summenzeichen in der Formel (5.2) durch ein Integralzeichen ersetzt:
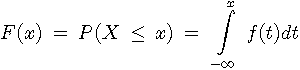 (5.5)
(5.5)
f(x), die erste Ableitung der Verteilungsfunktion, ist die Dichtefunktion :
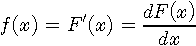 (5.6)
(5.6)
Beim Erwartungswert E(x) und bei der Varianz V(x) einer stetigen Zufallsvariable wird analog zu Verteilungsfunktion das Summenzeichen in den Formeln (5.3) und (5.4)durch ein Integralzeichen ersetzt:
Der Erwartungswert E(X) ist dann:
![]() (5.7)
(5.7)
für die Varianz V(X) gilt:
![]() (5.8)
(5.8)
Die bekannteste und für die Statistik wichtigste stetige Verteilung ist die Normalverteilung, die in Kapitel 7 ausführlich behandelt wird.
Allgemein kann man sagen, in der analytischen Statistik modelliert man stetige Merkmale durch stetige Zufallsvariable und diskrete Merkmale durch diskrete Zufallsvariable.
Beispiel 5.2
In einem Versuch sollen 10 Versuchstiere auf zwei Behandlungen A bzw. B verteilt werden. Jedem Behandlungsarm sollen 5 Versuchstiere zufällig zugeteilt werden. Der Versuchsleiter numeriert die Tiere von 1 bis 10 durch. Den Tieren mit den ungeraden Nummern 1, 3, 5, 7, 9 teilt er die Behandlung per Münzwurf zu (bei "Zahl" wird Therapie A zugeordnet, bei "Wappen" wird Therapie B zugeordnet).
Den Tieren mit den geraden Nummern 2, 4, 6, 8, 10 teilt er die jeweils andere Behandlung zu. Auf diese Weise ist die geforderte 5:5 Verteilung sichergestellt. Die Anzahl der Tiere mit ungerader Versuchsnummer, die der Behandlung A zugeteilt werden, ist eine diskrete Zufallsvariable X.
X, die Anzahl der Versuchstiere mit ungerader Nummer, denen die Behandlung A zugeteilt wird, kann die Werte 0, 1, 2, 3, 4 oder 5 annehmen
Die Menge S der möglichen Ergebnisse des fünfmaligen Münzwurfs, lässt sich als die Menge aller fünfstelligen Folgen (x1, x2, x3, x4, x5) schreiben, wobei xi entweder 0 oder 1 ist, je nachdem, ob im i-ten Versuch Wappen oder Zahl geworfen wurde (i=1,2,3,4,5).
Das so definierte S enthält 25 = 32 Elemente (= mögliche Ergebnisse).
Wenn man davon ausgeht, dass Wappen bzw. Zahl mit der gleichen Wahrscheinlichkeit geworfen werden, sind alle Ergebnisse in S gleichwahrscheinlich., und es gilt für jedes Ereignis {e} aus der Menge S:
P(e) = 1/32
5.4 Binomialkoeffizient
Die Anzahl der
Möglichkeiten aus n Dingen k auszuwählen,
wird mit ![]() -
gelesen n über k - bezeichnet und heißt Binomialkoeffizient. Beim
allwöchentlichen Zahlenlotto werden 6 aus 49 Kugeln
ausgewählt. Es gibt also
-
gelesen n über k - bezeichnet und heißt Binomialkoeffizient. Beim
allwöchentlichen Zahlenlotto werden 6 aus 49 Kugeln
ausgewählt. Es gibt also ![]() Möglichkeiten. Dies ist nur die
Schreibweise. Wenn man die Anzahl wirklich ausrechnen
will, benötigt man die Formel
Möglichkeiten. Dies ist nur die
Schreibweise. Wenn man die Anzahl wirklich ausrechnen
will, benötigt man die Formel
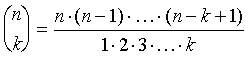 .
.
Eine Herleitung der Formel findet man in den einschlägigen Lehrbüchern. Beim Zahlenlotto wird daraus z. B.:
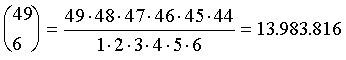 .
.
Es ist allgemein üblich, die Abkürzung
k! = 1.2.3.....k
(k! wird "k Fakultät" gelesen) zu verwenden. Mit dieser Abkürzung gilt
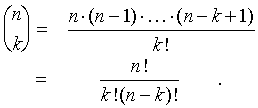
Aufgrund der obigen Definition gilt
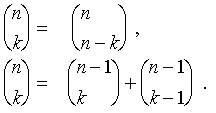
Mithilfe dieser Formeln und der Festlegung
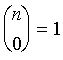
lassen sich die Binomialkoeffizienten rekursiv berechnen (Pascalsches Dreieck).
| 1 | ||||||||||||
| 1 | 1 | |||||||||||
| 1 | 2 | 1 | ||||||||||
| 1 | 3 | 3 | 1 | |||||||||
| 1 | 4 | 6 | 4 | 1 | ||||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 |
5.5 Bernoulli- und Binomialverteilung
Bernoulli- und Binomialverteilung sind zwei spezielle diskrete Wahrscheinlichkeitsverteilungen, die in den Anwendungen häufig auftreten. Deshalb sollen sie hier etwas ausführlicher betrachtet werden.
Es wird zwölfmal gewürfelt und gefragt, wie oft dabei eine 6 erscheint. Diese Anzahl X ist ein Beispiel für eine binomialverteilte Zufallsvariable mit den speziellen Parametern n=12 für die Anzahl der Würfe und p = 1/6 für die Wahrscheinlichkeit einer 6 in jedem einzelnen der 12 Würfe. Man schreibt abkürzend:
X: B(n=12 ; p=1/6)
Allgemein ergibt sich eine binomialverteilte Zufallsvariable X: B(n,p) unter folgenden Bedingungen:
- In einem Versuch tritt ein Ereignis A mit der Wahrscheinlichkeit P(A) =p ein. (Beim Würfeln ist das die 6, die mit der Wahrscheinlichkeit 1/6 gewürfelt wird).
- Dieser Versuch wird n-mal unter identischen Bedingungen wiederholt. (Im Beispiel wird 12-mal gewürfelt).
Die binomialverteilte Zufallsvariable X gibt an, wie oft A bei den n Versuchswiederholungen eintritt. X kann offenbar die Werte 0,1,...,n annehmen. X = n bedeutet, dass in allen n Versuchswiederholungen das Ereignis A eingetreten ist, z. B. dass in allen 12 Würfen die 6 gekommen ist. Das wäre zwar recht überraschend, aber keineswegs ausgeschlossen.
Man interessiert sich für die Wahrscheinlichkeit
P( X = k ) (k=0,1,...,n),
mit der X den möglichen Wert k annimmt.
Man findet
Der Beweis für diese Formel soll am Würfelbeispiel X: B(12 ; 1/6) kurz skizziert werden. Wir fragen beispielsweise nach P(X=3) . Jedes Ergebnis des 12-maligen Würfelns lässt sich durch eine 12-stellige Folge von 6 und ![]() beschreiben. Dabei steht '6' für das Würfeln einer 6 und '
beschreiben. Dabei steht '6' für das Würfeln einer 6 und '![]() ' für das Würfeln einer von 6 verschiedenen Zahl. Ein mögliches Ergebnis wäre z. B.
' für das Würfeln einer von 6 verschiedenen Zahl. Ein mögliches Ergebnis wäre z. B.
X=3 bedeutet dann, dass in dieser Folge genau dreimal eine 6 und 9-mal eine ![]() steht.
steht.
Es gibt ![]() verschiedene solcher Folgen, denn jede Folge entspricht genau einer Möglichkeit, aus den 12 Plätzen 3 auszuwählen und sie mit einer 6 zu besetzen.
verschiedene solcher Folgen, denn jede Folge entspricht genau einer Möglichkeit, aus den 12 Plätzen 3 auszuwählen und sie mit einer 6 zu besetzen.
Jede einzelne dieser ![]() Folgen hat wegen der Unabhängigkeit der Versuchswiederholungen die Wahrscheinlichkeit
Folgen hat wegen der Unabhängigkeit der Versuchswiederholungen die Wahrscheinlichkeit ![]() . Da das Ereignis {X=3} aus genau
. Da das Ereignis {X=3} aus genau ![]() solcher Folgen besteht, ergibt sich insgesamt
solcher Folgen besteht, ergibt sich insgesamt
,
genau wie es die Formel behauptet.
Das Ergebnis einer einzelnen der n Versuchswiederholungen lässt sich ebenfalls durch eine Zufallsvariable beschreiben:
.
Offenbar ist Yi:B(1,p) der Spezialfall für n=1 einer Binomialverteilung. Diesen Spezialfall nennt man Bernoulliverteilung. Aus der Definition folgt unmittelbar
;
d.h., jede Binomialverteilung ist als Summe von n unabhängigen Bernoulliverteilungen darstellbar.
Diese Tatsache hilft bei der Berechnung E(X) und V(X). Für die Bernoulliverteilung Yi folgt unmittelbar aus der Definition von Erwartungswert und Varianz.
Für den Erwartungswert E(X) folgt nun
.
Bei der Berechnung der Varianz V(X) macht man sich die - hier nicht bewiesene - Tatsache zunutze, dass sich die Varianzen unabhängiger Zufallsvariablen addieren, daher also
.
Die Abbildungen 5.3 bis 5.5 zeigen die Wahrscheinlichkeitsfunktionen der Binomialverteilungen B(10,0.3), B(10,0.5) und B(10,0.7). Man erkennt, dass sich der Gipfel der Verteilung mit wachsendem p nach rechts verlagert.
Beispiel 5.3
Ein Kinderarzt weiss aus Erfahrung, dass 20 % aller Neugeborenen nach unauffälliger Schwangerschaft weniger als 2500 g wiegen. Mehrlingsgeburten sind dabei ausgeschlossen. Aus den entsprechenden Geburtsprotokollen des vergangenen Jahres entnimmt er eine zufällige Stichprobe von n = 10 Protokollen. Die Anzahl der Protokolle, in denen ein Geburtsgewicht von weniger als 2500 g dokumentiert ist, ist eine diskrete binomialverteilte Zufallsvariable X. X kann die Werte 0,1,2,3,4,5,6,7,8,9,10 annehmen. Die Wahrscheinlichkeitsfunktion von X ist in Tabelle 5.1 zusehen, der Graph in Abbildung 5.6.
Tabelle 5.1: Wahrscheinlichkeitsfunktion von X
| k= | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| f(k)= | .10737 | .26844 | .30199 | .20133 | .08808 | .02642 | .00551 | .00079 | .00007 | .00000 | .00000 |
Der Arzt muss im Mittel mit n*p=10*0.2=2 Geburtsgewichten unter 2500g rechnen. Wann man an der Richtigkeit des Erfahrungswerts p=0.2 zu zweifeln beginnt, dürfte individuell verschieden sein.
In der Statistik ist die Konvention weit verbreitet, dann eine Theorie zu verwerfen, wenn sie dem tatsächlich beobachteten Ereignis eine Wahrscheinlichkeit von p<= 0.05 zuweist. Das ist hier der Fall, wenn in der Stichprobe von 10 Geburtsprotokollen mehr als 4 mit einem Geburtsgewicht unter 2500g vorkommen, wie man der folgenden Abbildung 5.7 und der anschließenden Javascript-Prozedur entnehmen kann.
 Applet - Binomial- und Poissonverteilung
Applet - Binomial- und Poissonverteilung
 Javascript und Applet - diskrete Verteilungen
Javascript und Applet - diskrete Verteilungen
Die soeben vorgestellte Binomialverteilung ist durch die beiden Parameter n und p definiert, wobei n die Anzahl der Wiederholungen eines Zufallsexperiments und p die Erfolgswahrscheinlichkeit für jedes einzelne Experiment ist. Die Poissonverteilung hat nur einen Parameter,![]() . Dabei ist sowohl der Erwartungswert als auch die Varianz gleich diesem Parameter.
. Dabei ist sowohl der Erwartungswert als auch die Varianz gleich diesem Parameter.
Die Poissonverteilung gilt für seltene Ereignisse, die unabhängig voneinander auftreten. In einem solchen Fall entspricht die Binomialverteilung mit großem n und kleinem p näherungsweise einer Poissonverteilung mit Parameter ![]() = n . p, dem Erwartungswert der Binomialverteilung.
= n . p, dem Erwartungswert der Binomialverteilung.
Die Wahrscheinlichkeitsfunktion der Poissonverteilung lautet:
k=0,1,2,3.....
Beispiel 5.4
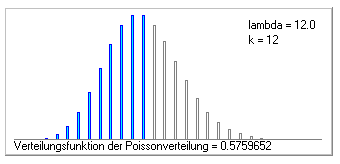
Die mittlere Anzahl dem Kinderkrebsregister in Mainz gemeldeter Malignome betrug in den letzten zehn Jahren etwa 12 Fälle pro Jahr auf 100000 Kinder. Die Binomialverteilung mit n=100000 und p=12/100000 gibt an, wie groß die Wahrscheinlichkeit ist, dass z.B. im kommenden Jahr k=0,1,2,... Fälle pro 100000 Kinder gemeldet werden. Die Wahrscheinlichkeit für z.B. k=12 Fälle beträgt nach der Formel für die Binomialverteilung 0.11437478.
Für die Poissonverteilung mit dem Parameter
= (12/100000)*100000 = 12 ergibt sich mit 0.11436792 nahezu der gleiche Wert.
Abbildung 5.8: Wahrscheinlichkeitsfunktion der Poissonverteilung mit = 12
 Applet - Binomial- und Poissonverteilung
Applet - Binomial- und Poissonverteilung
 Javascript und Applet - diskrete Verteilungen
Javascript und Applet - diskrete Verteilungen
5.7 Schätzen von p
Bei den bisherigen Überlegungen ging man davon aus, dass p, die Wahrscheinlichkeit für das Eintreten des Ereignisses A, bekannt ist. In den meisten Anwendungen ist das aber nicht der Fall, und die beschriebenen Versuche werden durchgeführt, um p aufgrund des Versuchsergebnisses zu schätzen. Wenn das Ereignis A bei den n Versuchswiederholungen k-mal eingetreten ist, schätzt man p durch
Die Bezeichnung ![]() (gelesen "p - Dach") für den Schätzwert ist allgemein üblich. Bei genauem Hinsehen erkennt man, dass der Schätzwert Realisation der Zufallsvariablen
(gelesen "p - Dach") für den Schätzwert ist allgemein üblich. Bei genauem Hinsehen erkennt man, dass der Schätzwert Realisation der Zufallsvariablen
ist, wobei X die oben bereits eingeführte Zufallsvariable ist, die angibt, wie oft A bei den n Versuchswiederholungen eintritt. H ist nichts anderes als die relative Häufigkeit, mit der A in den n Versuchswiederholungen eintritt. Nach den Rechenregeln für Erwartungswert und Varianz bestimmt man
Das sind zwei erfreuliche und starke Ergebnisse. Das erste besagt, dass der Erwartungswert der Zufallsvariablen H, die man zum Schätzen von p verwendet, gleich dem Wert ist, den man schätzen will. Eine Schätzung, die diese Eigenschaft besitzt, nennt man erwartungstreu oder auch unverzerrt (engl.: unbiased).
Das zweite Ergebnis besagt, dass die erwartete quadratische Abweichung der Schätzung von ihrem Erwartungswert mit wachsendem n gegen Null geht. Das ist eine weitere Version des Gesetzes der großen Zahl (vgl. Kap. 4.7).
Beispiel 5.5
Der Erfahrungswert von p=0.2 für die Geburtsgewichte unter 2500 g erscheint Ihnen nicht richtig. Sie wollen ihn aus Ihren Daten selber schätzen. Wenn Sie bei n=10 Protokollen k=3 Geburtsgewichte unter 2500 g gefunden haben, erhalten Sie mit der relativen Häufigkeit einen Schätzwert für p die Wahrscheinlichkeit:
Um die Genauigkeit der Schätzung zu verbessern, muss man den Stichprobenumfang vergrößern. Dies ist aus den obigen Formeln für den Erwartungswert und die Varianz ersichtlich. Der Erwartungswert der Schätzung entspricht dem wahren Wert (unverzerrte Schätzung) und die Varianz der Schätzung konvergiert mit wachsendem n gegen Null.= 3/10 = 0.3.

Applet - Relative Häufigkeit und Wahrscheinlichkeit
Applet - Binomial- und Poissonverteilung