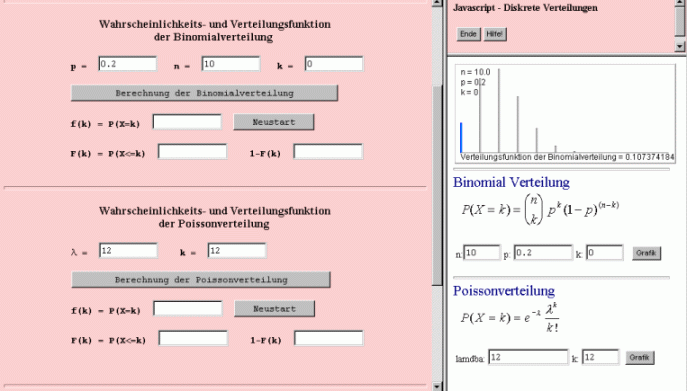
Nach Aufruf des Javascript/Applets "Diskrete Verteilungen" erscheint folgendes Bild.
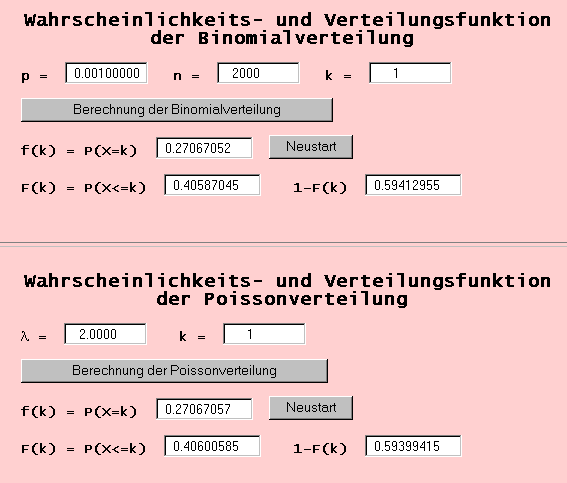
Aus den Zahlenangaben der Aufgabe 1 ergeben sich für die Binomialverteilung die Parameter n=2000 und p=1/1000=0.001 und für die Poissonverteilung der Parameter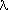 
=2000/1000=2.
Für die Anzahl k der Kinder mit Down Syndrom errechnet sich für k=0 der gesuchte Wert der Wahrscheinlichkeitsfunktion P(X=k) als 0.13519993 (Binomialverteilung) bzw. 0.13533528 (Poissonverteilung).
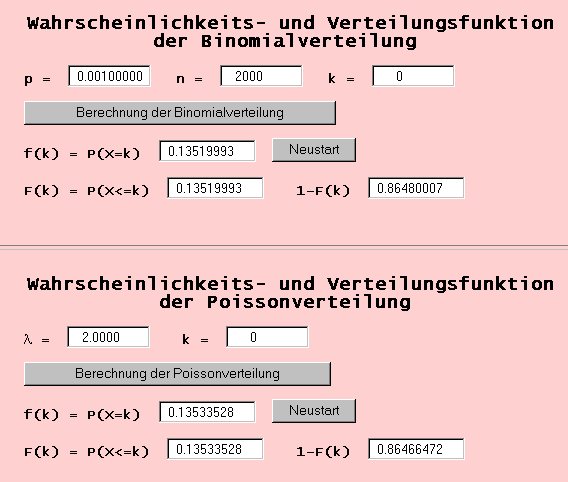
Entsprechend kann man die Werte für k=1,...,6 berechnen.
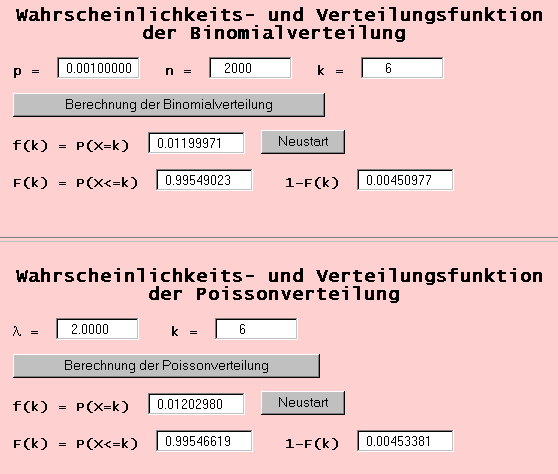
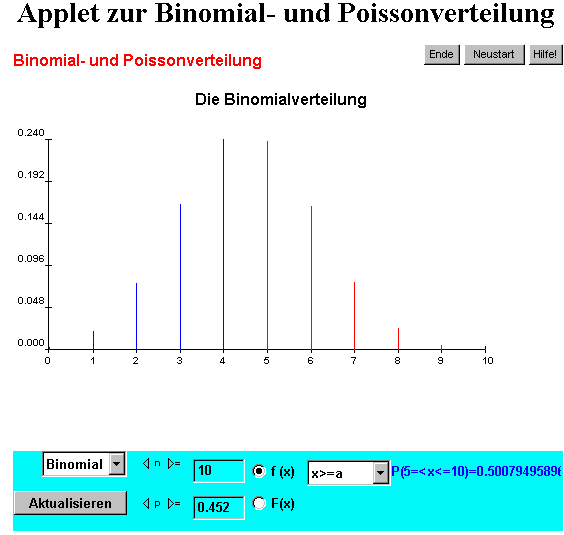
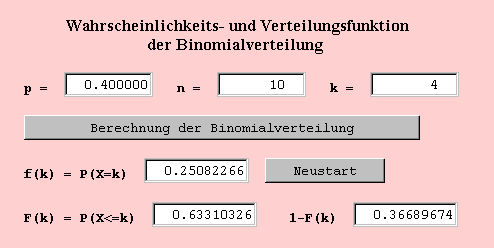
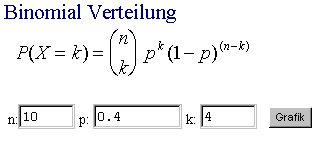
Aus den Zahlenangaben der Aufgabe 2 ergeben sich für die Binomialverteilung die Parameter n=10 und p=0.4.
Für alle Werte von k k=0,....,10 kann man nun die Berechnungen vornehmen.
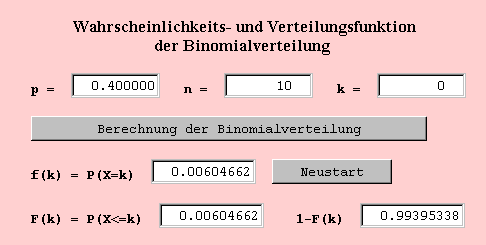
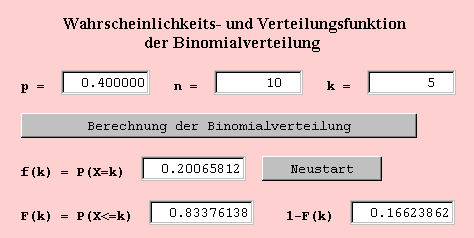
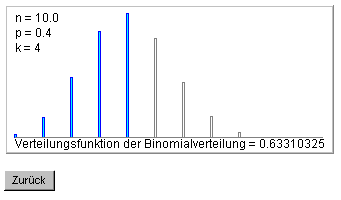
Zur Beantwortung der Frage nach der Wahrscheinlichkeit P(X>=5) wird die Berechnung für k=4 durchgeführt. Die Wahrscheinlichkeit F(4)=P(X<=4) ist dann 0.63310326 und die Gegenwahrscheinlichkeit 1-F(4)=0.36689674 ist dann die gesuchte Wahrscheinlichkeit.
Zur Beantwortung der Frage 2c) kann man den Parameter p z.B. auf p=0.45 erhöhen. Die Wahrscheinlichkeit für P(X>=5) liegt noch knapp unter 0.5
Auch mit p=0.451 hat man die gesuchten 50% noch nicht erreicht.
Mit p=0.452 wird das Ziel erreicht.
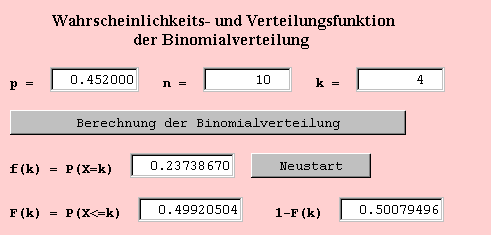
Zum gleichen Ergebnis wäre man auch mit dem Applet zur Binomial- und Poissonverteilung gekommen.
