4 Wahrscheinlichkeitsrechnung
- Grundbegriffe der Wahrscheinlichkeitsrechnung
- Zufallsexperiment
- Ergebnisse
- Ereignisse
- Axiome von Kolmogoroff
- Wahrscheinlichkeit von Ereignissen
- Venn-Diagramme
- Bedingte Wahrscheinlichkeiten
- Sensitivität und Spezifität
- Unabhängigkeit von Ereignissen
- Gesetz der großen Zahl
4.2 Zufallsexperiment und mögliche Ergebnisse
Grundlage der modernen Wahrscheinlichkeitsrechnung sind die Axiome von Kolmogoroff. Kolmogoroff geht von einem Zufallsexperiment aus, das im Prinzip unter gleichen Bedingungen beliebig oft wiederholt werden kann.
Trotz der gleichen Bedingungen ist das Ergebnis des Experiments von Wiederholung zu Wiederholung nicht vorhersehbar. Es gibt vielmehr eine ganze Menge möglicher Ergebnisse, die hier im folgenden mit S bezeichnet wird. Die einzelnen Ergebnisse werden mit e1,e2,... bezeichnet, d.h.
S = {e1,e2,...} .
Beispiel 4.1
Typische Zufallsexperimente sind das Würfeln,
das Werfen von Münzen,
die Ziehung von numerierten Kugeln aus einer Urne wie beim Lotto
oder das Austeilen von Karten beim Skat.
In all diesen Beispielen wird das für ein Zufallsexperiment Typische deutlich: es ist im Prinzip unter gleichen Bedingungen beliebig oft wiederholbar, das Ergebnis jeder einzelnen Wiederholung ist nicht vorhersehbar.
Die Menge der möglichen Ergebnisse ist z.B.
beim Münzwurf S={Wappen,Zahl}
beim Würfel S={1,2,3,4,5,6}
4.3 Ereignisse, Wahrscheinlichkeit von Ereignissen
Teilmengen von S, der Menge der möglichen Ergebnisse, bezeichnet man als Ereignisse. Durch diese Definition ist es möglich geworden, mit Ereignissen wie mit Mengen zu rechnen. Dabei werden die aus der Mengenlehre vertrauten Symbole benutzt.
Ereignisse, die nur ein mögliches Ergebnis enthalten, nennt man Elementarereignisse. Die Grundmenge S heißt sicheres Ereignis, die Menge, die kein mögliches Ergebnis enthält, heißt unmögliches Ereignis und wird, wie in der Mengenlehre üblich, mit Ø bezeichnet
A und B seien zwei
Ereignisse.
A A Eine Menge von Ereignissen A1,A2,......,Ak ist eine Zerlegung von S, wenn die Ereignisse Ai disjunkt sind und ihre Vereinigung S ergibt, d.h. Ai Vor diesem Hintergrund führte
Kolmogoroff den Begriff der Wahrscheinlichkeit eines Ereignisses ein und formulierte die
folgenden drei Axiome, die die Grundlage für das Rechnen
mit Wahrscheinlichkeiten bilden: Axiome von Kolmogoroff Es sei S die Menge der möglichen
Ergebnisse eines Versuchs, A, B seien Ereignisse, d. h.
Teilmengen von S. Mit P(A) wird die Wahrscheinlichkeit eines Ereignisses A bezeichnet (P von engl.: probability). Unter diesen Voraussetzung gelten die
Axiome: 1. Für jedes Ereignis A gilt: P(A) 2. Für das sichere Ereignis S gilt: P(S) = 1, 3. Sind die Ereignisse A und B disjunkt (A Aus den Axiomen folgt:
Für beliebige Ereignisse A und B gilt der Additionssatz:
4.4 Venn-Diagramme Das Rechnen mit Wahrscheinlichkeiten
lässt sich gut anhand von sogenannten Venn-Diagrammen
veranschaulichen. Abbildung 4.1 zeigt das Venn-Diagramm einer
Menge S, die aus 10 gleichwahrscheinlichen
Elementen besteht, sowie zwei Ereignisse A und B. Abbildung 4.1
Venn-Diagramm
Dann bezeichnet 
, gelesen A
quer, das Komplement von A. ist also
das Ereignis, dass A nicht eintritt.
B
ist
die Vereinigung von A und B und bezeichnet
das Ereignis, dass A oder B eintritt.
B
ist der Durchschnitt von A und B und
bezeichnet das Ereignis, dass A und B
gemeinsam eintreten.
Aj = Ø (i 
j), Ai = S.
.
0, B = Ø), dann gilt: P(A B) = P(A) + P(B),
P(
) = 1 - P(A).P(A
B) = P(A) + P(B) - P(A B).
Applet - Wahrscheinlichkeit von Ereignissen
Applet - Durchschnitt und Wahrscheinlichkeiten
Applet - Vereinigung und Wahrscheinlichkeiten
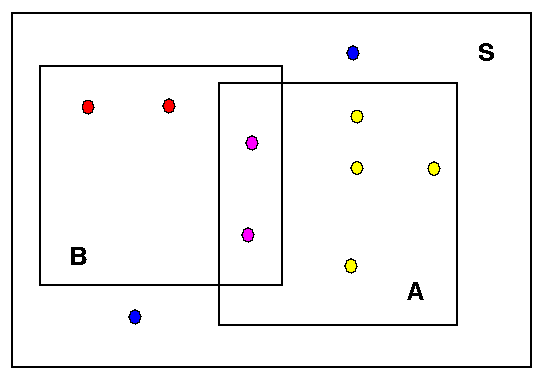
Beispiel 4.2
Für die Ereignisse A und B aus der Abbildung 4.1 gilt:
P(A) = 0.6
P(B) = 0.4
P(A
P(A
P(
4.5 Bedingte Wahrscheinlichkeiten, Bayessche Formel
Beim Würfeln mit einem idealen Würfel ist die Wahrscheinlichkeit für eine 6 unter der Bedingung, dass eine gerade Zahl gewürfelt wird, offenbar 1/3, denn 6 ist eine der drei gleichwahrscheinlichen Möglichkeiten 2, 4, 6.
Dies ist ein Beispiel für die bedingte Wahrscheinlichkeit P(A|B) eines Ereignisses A - hier Würfeln einer 6 - unter der Bedingung des Ereignisses B - hier Würfeln einer geraden Zahl. Die allgemeine Definition lautet:
.
Im Beispiel gilt P(A) = 1/6, P(B) = 1/2 und P(A
Im typischen medizinischen Anwendungsbeispiel ist A eine Krankheit - z. B. Masern - und B ein Symptom - z. B. roter Hautausschlag -. In diesem Fall ist P(A|B) die bedingte Wahrscheinlichkeit für Masern bei rotem Hautausschlag. Den Arzt, der den roten Ausschlag beim Patienten sieht, interessiert bei der Diagnosestellung diese bedingte Wahrscheinlichkeit und nicht etwa die unbedingte Wahrscheinlichkeit für Masern.
Wenn man die Rollen von A und B vertauscht, fragt man nach der bedingten Wahrscheinlichkeit von P(B|A), d. h. nach der bedingten Wahrscheinlichkeit von rotem Hautausschlag bei Masern. Die Formel von Bayes stellt den Zusammenhang zwischen diesen beiden bedingten Wahrscheinlichkeiten her. Durch Auflösen der Definitionsgleichung nach P(A
P(A|B) × P(B) = P(A
und damit
.
Wegen
erhält man hieraus schließlich die Bayessche Formel:
.
Im betrachteten Beispiel sagt diese Formel, dass man die bedingte Wahrscheinlichkeit P(A|B) von Masern bei rotem Ausschlag berechnen kann, wenn man die Wahrscheinlichkeit P(A) für Masern und die bedingten Wahrscheinlichkeiten des Symptoms ‘roter Hautausschlag’ für Patienten mit und Patienten ohne Masern kennt.
Man interpretiert dies als Berechnung der a-posteriori Wahrscheinlichkeit P(A|B) aus der a-priori Wahrscheinlichkeit P(A).
Beispiel 4.3
Ein Arzt in einer Rheuma-Ambulanz betreut im Jahr etwa 200 Patienten jüngeren und mittleren Lebensalters mit chronischen Rückenschmerzen, die nicht eindeutig auf einen Bandscheibenvorfall zurückzuführen sind. Aus langjähriger Erfahrung weiß der Arzt, dass bei etwa 60% der Patienten mit diesem Krankheitsbild ein Morbus Bechterew (K+) vorliegt. Um die Sicherheit bezüglich der Diagnose zu verbessern, könnte er eine HLA-Typisierung durchführen lassen. Er weiß, dass 95% aller Patienten mit einem Morbus Bechterew (K+) das HLA-Antigen B 27 ((T+) haben, das in der übrigen Bevölkerung (K-) nur mit einem Anteil von 8% vorkommt. Wie ändert sich die Sicherheit, nachdem dem Arzt das Ergebnis der Typisierung bekannt ist?
Aus den obigen Angaben ergeben sich die folgenden Wahrscheinlichkeiten:
P(K+) = 0.6, P(K-) = 0.4
P(T+|K+) = 0.95, P(T+|K-) = 0.08
Die gesuchte Wahrscheinlichkeit P(K+|T+) ist dann nach der Formel von Bayes P(K+|T+) = (0.95*0.6)/(0.95*0.6+0.08*0.4) = 0.947.
Dies bedeutet, dass in etwa 95% der Fälle mit einem positiven Testergebnis (HLA B 27-Antigen vorhanden) ein Morbus Bechterew vorliegen wird.
4.6 Sensitivität und Spezifität
Tabelle 4.1: Sensitivität und Spezifität beim klinischen Test
Testergebnis T Wirklichkeit W infiziert nicht infiziert Summe positiv 900 9 900 10 800 negativ 100 89 100 89 200 Summe 1 000 99 000 100 000 In einer fiktiven Grundgesamtheit von 100 000 Personen sind 1 000 Personen mit einem bestimmten Virus infiziert. Es gibt einen klinischen Test, mit dem man dies feststellen kann. Dieser Test ist allerdings nicht hundertprozentig sicher. Es werden nur 90 % der tatsächlich infizierten Personen im Test als positiv erkannt (Sensitivität), und genauso sind nur 90 % der nicht infizierten Personen im Test negativ (Spezifität).
Die Verhältnisse sind in Tabelle 4.1 tabellarisch dargestellt.
Sensitivität und Spezifität sind in der Sprache der Wahrscheinlichkeitsrechnung nichts anderes als bedingte Wahrscheinlichkeiten:
Sensitivität: P( T=+ | W=+) = 900/1000 = 0.9
Spezifität: P(T=- | W=-) = 89100/99000 = 0.9
In der Praxis möchte man umgekehrt auch wissen, wie groß bei gegebener Sensitivität und Spezifität die Wahrscheinlichkeit ist, dass ein im Test positiver Patient tatsächlich infiziert ist, bzw. ein im Test negativer Patient tatsächlich nicht infiziert ist. Diese bedingten Wahrscheinlichkeiten nennt man "positiven" bzw. "negativen" prädiktiven Wert
Für diese beiden bedingten Wahrscheinlichkeiten gilt:
Positiver prädiktiver Wert: P(W=+ | T=+) = 900/10800 = 0.0833, d.h. nur 8.3% der Personen mit einem positiven Test sind tatsächlich auch mit dem Virus infiziert.
Negativer prädiktiver Wert: P(W=- | T=-) = 89100/89200 = 0.9989
Außer von der Sensitivität und der Spezifität hängen der positive bzw. negative prädiktive Wert noch von der Wahrscheinlichkeit P(W=+) der Prävalenz der Krankheit ab.
Weitere Kennzahlen zur Beurteilung eines diagnostischen Verfahrens sind die Wahrscheinlichkeiten für einen falsch positiven bzw. falsch negativen Wert.
Für diese beiden Wahrscheinlichkeiten gilt:
Falsch positiver Wert: P({W=-}
Falsch negativer Wert: P({W=+}
Beispiel 4.4
Das Bakterium Helicobacter Pylori spielt eine wesentliche Rolle bei der Enstehung von Ulzera (Geschwüren) im Magen. In Deutschland sind etwa 20% der Erwachsenen unter 40 Jahren mit diesem Bakterium infiziert.
Der sogenannte CLO-Test war der erste diagnostische Test zum Nachweis von Helicobacter Pylori. Der Test ist seit 1988 im Einsatz und hat eine Sensitivität von 98% und eine Spezifität von 97%.
Für ein Screening von 1000 Erwachsenen unter 40 Jahren ergibt sich aus den Angaben folgende Tabelle:
Testergebnis T Wirklichkeit W infiziert nicht infiziert Summe positiv 196 24 220 negativ 4 776 780 Summe 200 800 1000 Damit erhält man die folgenden weiteren Kennzahlen:
Positiver prädiktiver Wert: P(W=+ | T=+) = 196/220 = 0.8909, d.h. 89.1% der Personen mit einem positiven Test sind tatsächlich auch mit dem Bakterium infiziert.
Negativer prädiktiver Wert: P(W=- | T=-) = 766/780 = 0.99487, d.h. 99.5% der Personen mit einem negativen Test sind tatsächlich auch nicht mit dem Bakterium infiziert.
Falsch positiver Wert: P({W=-}
Falsch negativer Wert: P({W=+}
4.7 Unabhängigkeit von Ereignissen
Der Begriff Unabhängigkeit von Ereignissen spielt in den Anwendungen eine wichtige Rolle. Zwei Ereignisse A und B heißen unabhängig voneinander, wenn
P(A|B) = P(A)
gilt.
Nach Definition der bedingten Wahrscheinlichkeit ist die Definition gleichwertig mit
P(A
d. h., die Wahrscheinlichkeit für das gemeinsame Eintreten zweier unabhängiger Ereignisse entspricht dem Produkt der beiden Einzelwahrscheinlichkeiten. Man nennt dies auch den Multiplikationssatz der Wahrscheinlichkeitsrechnung.
Wenn man allein die mathematische Seite des Problems betrachtet, ist die Frage nach der Unabhängigkeit zweier Ereignisse A und B leicht zu beantworten. Man hat nur zu überprüfen ob
P(A
gilt oder nicht.
Für den Biometriker besteht aber das Problem darin, ob er in einem der folgenden Beispiele zur Auswertung ein mathematisches Modell ansetzen darf, das Unabhängigkeit voraussetzt, oder ob er das nicht darf.
Beispiel 4.5
1) Das Geschlecht von Kind 1 und Geschlecht von Kind 2 bei zwei Kindern des gleichen Elternpaares sind unabhängig (?).
2) Die Dauer der Geburt und die Art der Narkose sind nicht unabhängig.
3) Die Dauer der Geburt und das Alter der Mutter sind nicht unabhängig.
4) Die Dauer der Geburt und die Parität der Mutter sind nicht unabhängig.
5) Die Dauer der Geburt und das Alter des Vaters sind unabhängig (?).
6) Die Augenfarbe und die Haarfarbe einer Person sind nicht unabhängig (?).
7) Lebenserwartung und Geschlecht sind nicht unabhängig.
8) Studienfach und Geschlecht sind nicht unabhängig.Unbekannte Wahrscheinlichkeiten schätzt man durch die relativen Häufigkeiten aus einer zufälligen Stichprobe. Theoretische Grundlage hierfür ist das Gesetz der großen Zahl.
A sei ein Ereignis mit der Wahrscheinlichkeit P(A). nA sei die absolute Häufigkeit mit der A in n unabhängigen Versuchswiederholungen eintritt.
Das Gesetz der großen Zahl besagt:
,
d.h., die relative Häufigkeit, mit der ein Ereignis A in n unabhängigen Versuchswiederholungen eintritt, strebt mit wachsendem n gegen die Wahrscheinlichkeit des Ereignisses A.
Beispiel 4.6
Die relative Häufigkeit, mit der man bei Neugeborenen ein Geburtsgewicht unter 3000 g beobachtet, strebt mit wachsender Anzahl n der ausgewerteten Geburten gegen die Wahrscheinlichkeit dieses Ereignisses.
Applet-Wahrscheinlichkeit von Ereignissen
Applet-Bedingte Wahrscheinlichkeiten
Applet-Durchschnitt und Wahrscheinlichkeit
Applet-Vereinigung und Wahrscheinlichkeit
Vierfeldertafel - Sensitivität, Spezifität (Javascript)
Applet-Gesetz der großen Zahl - Stichproben
Applet-Gesetz der großen Zahl - Würfeln
