Nach Aufruf des Applets "Explorative Datenanalyse" erscheint folgendes Bild.
Um den Datensatz "aml1.html" zu laden, muss dieser Text am unteren Rand des Applets im Eingabefeld "Sonstiger Datensatz" eingegeben werden, durch Mausklick rechts unten die Option "Sonstiger Datensatz" aktiviert werden und die Taste "Datensatz laden" angeklickt werden.
Es wird dann der gewünschte Datensatz mit 727 Patienten und 36 Variablen geladen und steht zur weiteren Analyse mit Hilfe des Applets zur Verfügung.
Um die gewünschten bedingten Wahrscheinlichkeiten zu schätzen, wird die Option "Kontingenztafel" angeklickt.
Es erscheint dann folgendes Bild. In der Bildmitte wird die Kodierung der Merkmalsausprägungen der qualitativen Merkmale erläutert (z.B. 1=männlich, 2=weiblich für das Merkmal Geschlecht).
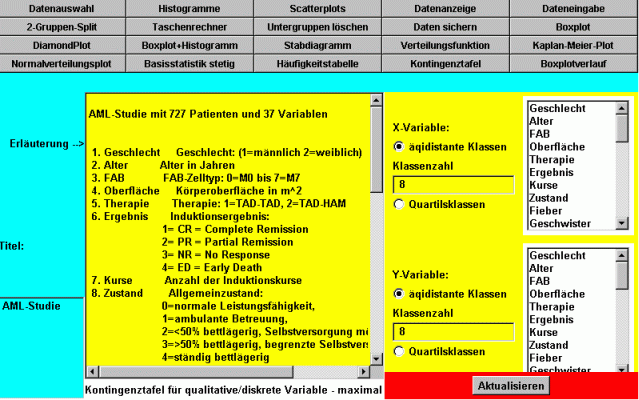
Man kann nun am rechten Rand die gewünschten qualitativen Variable durch Mausklick auswählen.
Nach Anklicken der Taste "Aktualisieren" erhält man in einem separaten Fenster die gewünschten Ergebnisse.
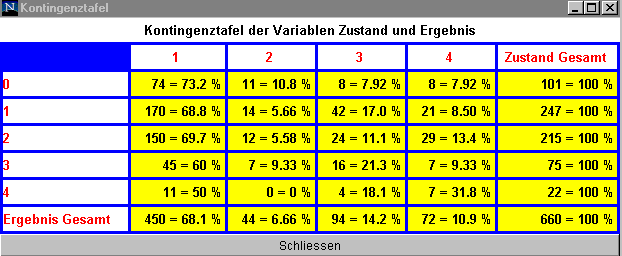
Es gibt 74 Patienten mit der Auprägung A= Ergebnis =1 = CR und B = Zustand = 0= normale Leistungsfähigkeit. Man erhält als Schätzer für die Wahrscheinlichkeit P(A
B) = 74/660 = 0.1121. Die Wahrscheinlichkeit P(B) beträgt dann 101/660=0.153. Die bedingte Wahrscheinlichkeit P(A|B) ist dann P(A|B)= P(AB)/P(B) = 74/101 = 0.7327.
Es gibt 7 Patienten mit der Auprägung A= Ergebnis =4 = ED (Early Death) und B = Zustand = 4= ständig bettlägrig. Man erhält als Schätzer für die Wahrscheinlichkeit P(AB) = 7/660 = 0.0106. Die Wahrscheinlichkeit P(B) beträgt dann 22/660=0.0333. Die bedingte Wahrscheinlichkeit P(A|B) ist dann P(A|B)= P(AB)/P(B) = 7/22 = 0.3182.
Zur Beantwortung der nächsten Frage wird die Variable Alter mit der Option "Quartilsklassen" und die Variable Ergebnis ausgewählt
Nach Anklicken der Leiste "Aktualisieren" erhält man das folgende Bild
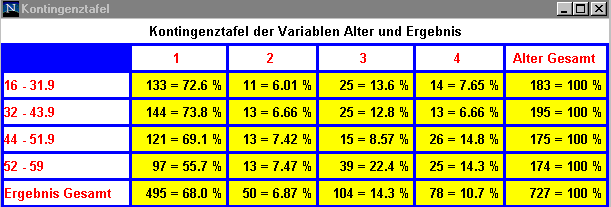
Die gewünschte bedingte Wahrscheinlichkeit P(Ergebnis =CR | Alter >= 52) ist dann 97/174=0.5575.
Bei der Auswahl der Variablen FAB-Zelltyp ist darauf zu achten, dass man wieder mit der Option "Äquidistante Klassen " arbeitet.
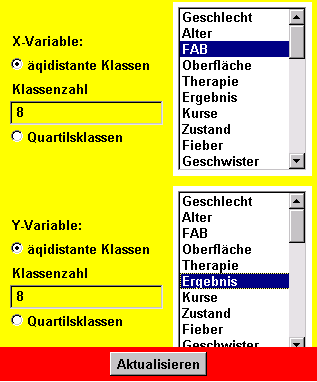
Nach Anklicken der Leiste "Aktualisieren" erhält man das folgende Bild
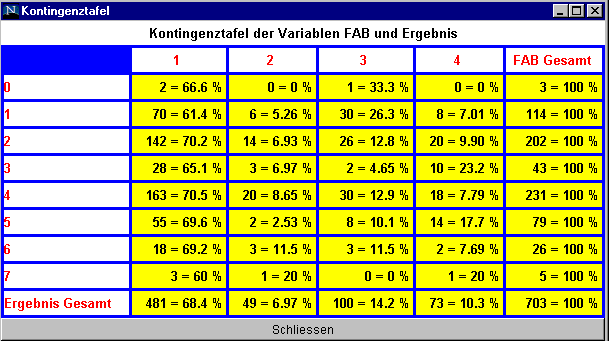
Die gewünschte bedingte Wahrscheinlichkeit P(Ergebnis =ED | FAB-Zelltyp = M3) ist dann 10/43=0.232.
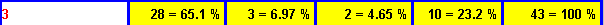
Zur Beantwortung der nächsten Frage werden die Variablen Kurse und Ergebnis ausgewählt.
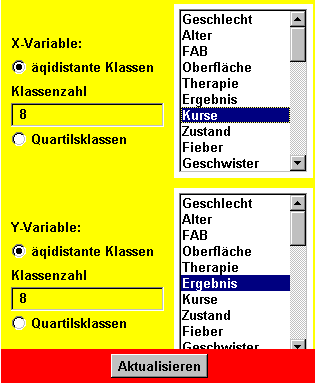
Nach Anklicken der Leiste "Aktualisieren" erhält man das folgende Bild
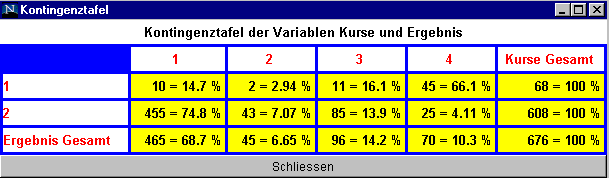
Die gewünschte bedingte Wahrscheinlichkeit P(Ergebnis =ED | Anzahl der Kurse =1) ist dann 45/68=0.661.
Zur Beantwortung der ersten Frage nach der Unabhängigkeit der Ereignisse A und B wird die Kontingenztafel Geschlecht vs. Ergebnis berechnet.
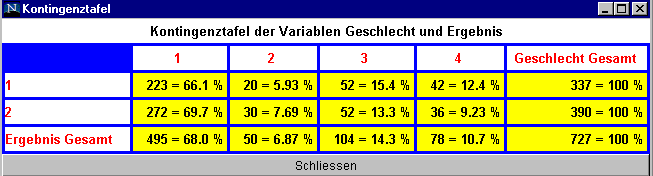
Es gibt 223 Patienten mit der Auprägung A= Geschlecht =1 = männlich und B = Ergebnis = 1 = CR . Man erhält als Schätzer für die Wahrscheinlichkeit P(AB) =223/727 = 0.3067. Die Wahrscheinlichkeiten P(A) bzw. P(B) betragen dann 337/727=0.4635 bzw. 495/727=0.6809. Das Produkt der Wahrscheinlichkeiten P(A)xP(B) ist dann = 0.3156 und damit nur geringfügig größer als die Wahrscheinlichkeit P(AB). Mann kann damit annehmen, dass A und B unabhängig sind.
Zur Beantwortung der nächsten Frage werden die Variablen Größe mit der Option "Quartilsklassen" und Ergebnis ausgewählt.
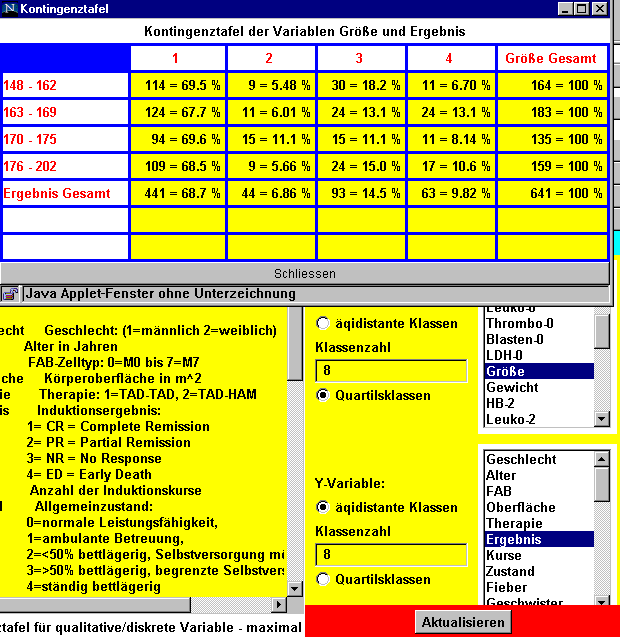
Es gibt 114 Patienten mit der Auprägung A= Größe <= 162 und B = Ergebnis = 1 = CR . Man erhält als Schätzer für die Wahrscheinlichkeit P(AB) =114/641 = 0.1778. Die Wahrscheinlichkeiten P(A) bzw. P(B) betragen dann 164/641=0.2558 bzw. 441/641=0.6880. Das Produkt der Wahrscheinlichkeiten P(A)xP(B) ist dann = 0.1760 und damit nur geringfügig kleiner als die Wahrscheinlichkeit P(AB). Mann kann damit annehmen, dass A und B unabhängig sind.
Zur Beantwortung der nächsten Frage werden die Variablen Gewicht mit der Option "Quartilsklassen" und Ergebnis ausgewählt.
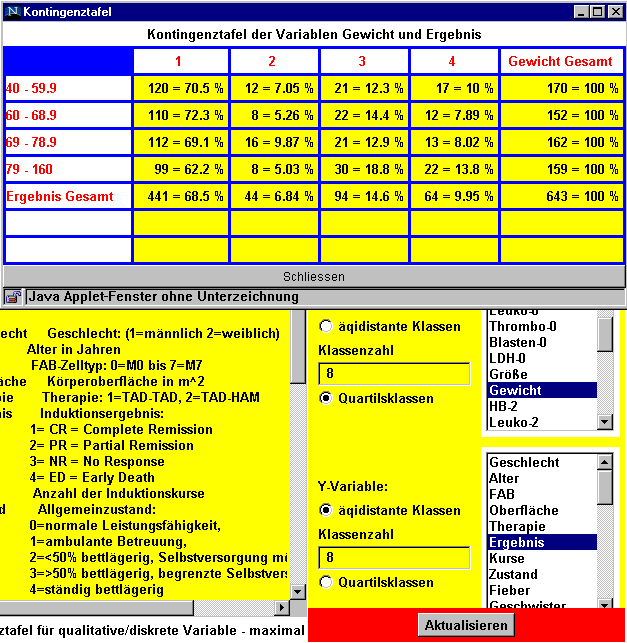
Es gibt 22 Patienten mit der Auprägung A= Gewicht >=79 und B = Ergebnis = 4 = ED . Man erhält als Schätzer für die Wahrscheinlichkeit P(AB) =22/643 = 0.0342. Die Wahrscheinlichkeiten P(A) bzw. P(B) betragen dann 159/643=0.2473 bzw. 64/643=0.0.0995. Das Produkt der Wahrscheinlichkeiten P(A)xP(B) ist dann = 0.0246 und damit kleiner als die Wahrscheinlichkeit P(AB) = 0.0342. Mann kann damit annehmen, dass A und B nicht unabhängig sind.
Zur Beantwortung der nächsten Frage werden die Variablen Kurse mit der Option "Äquidistante Klassen" und Ergebnis ausgewählt.
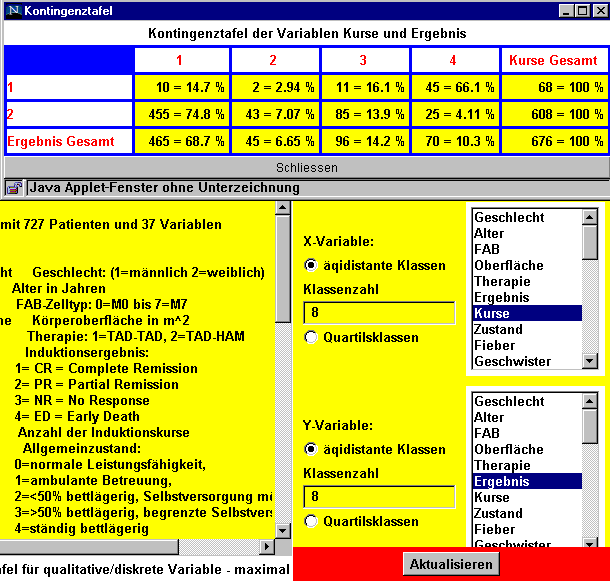
Es gibt 45 Patienten mit der Auprägung A = Kurse=1 und B = Ergebnis = 4 = ED . Man erhält als Schätzer für die Wahrscheinlichkeit P(AB) =45/676 = 0.0666. Die Wahrscheinlichkeiten P(A) bzw. P(B) betragen dann 68/676=0.1006 bzw. 70/676=0.0.1036. Das Produkt der Wahrscheinlichkeiten P(A)xP(B) ist dann = 0.1042 und damit deutlich größer als die Wahrscheinlichkeit P(AB) = 0.0666. Mann kann damit annehmen, dass A und B nicht unabhängig sind.
Nach Aufrufen der Javacript-Prozedur - Vierfeldertafel erscheint folgendes Bild.
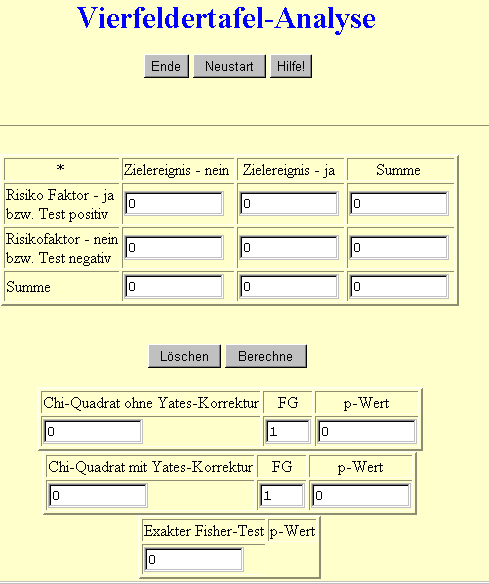
Die Daten der beiden diagnostischen Verfahren Klinische Diagnose vs. Rachenabstrich sind wie folgt einzugeben.
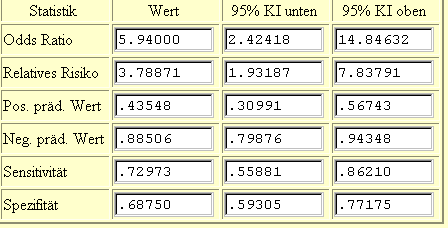
Nach Ankicken der Taste "Berechnen" erhält man folgendes Ergebnis für die gesuchten Werte Sensitivität, Spezifität, positiver und negativer prädiktiver Wert.
Nach Aufruf des Applets "Schachtelspiel" erscheint folgendes Bild.
