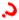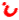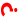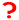Applet - Explorative Datenanalyse -- Datensatz "AML" - Kontingenztafel "Therapie" gegen "Ergebnis"
Applet - Explorative Datenanalyse -- Datensatz "AML" - Kontingenztafel "Therapie" gegen "Ergebnis"
3.3 Regression und Korrelation
An n Beobachtungseinheiten werden zwei stetige Merkmale X und Y beobachtet, die nicht klassiert werden. Es ist ratsam, die Untersuchung der gemeinsamen Verteilung zweier stetiger Merkmale mit der Zeichnung einer Punktwolke (Scatterplot) zu beginnen; denn die Punktwolke liefert auf einen Blick Informationen, die für das weitere Vorgehen wichtig sind. Dazu trägt man das Merkmal X an der x-Achse, das Merkmal Y an der y-Achse ab und zeichnet das an der i-ten Beobachtungseinheit festgestellte Wertepaar (x,i, yi) als Punkt in das Koordinatensystem ein (i=1,2,....,n). Jede Beobachtungseinheit liefert also genau einen Punkt für die Punktwolke.
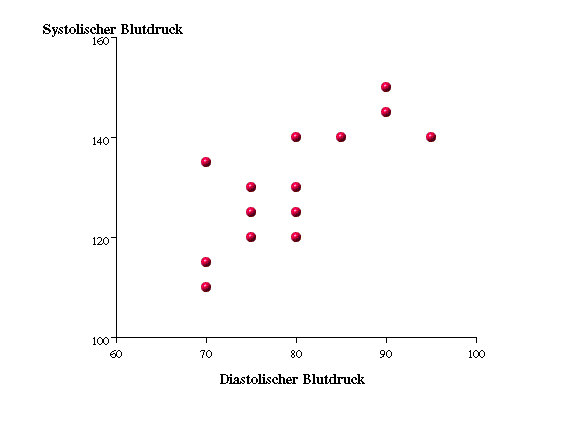
Tabelle 3.5 enthält von 15 Patienten die Angaben zum diastolischen und zum systolischen Blutdruck, die in Abbildung 3.1 als Punktwolke dargestellt sind. Der diastolische Blutdruck (RRdias) ist an der x-Achse, der systolische (RRsys) an der y-Achse abgetragen.
Tabelle 3.5: Diastolischer und systolischer Blutdruck von 15 Patienten
Lfd. Nr. |
RRdias |
RRsys |
1 |
80 |
120 |
2 |
70 |
115 |
3 |
80 |
125 |
4 |
70 |
110 |
5 |
70 |
115 |
6 |
80 |
130 |
7 |
85 |
140 |
8 |
75 |
120 |
9 |
75 |
125 |
10 |
90 |
150 |
11 |
80 |
140 |
12 |
70 |
135 |
13 |
95 |
140 |
14 |
75 |
130 |
15 |
90 |
145 |
Abbildung 3.1: Punktwolke Diastolischer und systolischer Blutdruck
 Applet - Explorative Datenanalyse -- Datensatz "Blutdruck" - Scatterplot "RRdias" gegen "RRsyst"
Applet - Explorative Datenanalyse -- Datensatz "Blutdruck" - Scatterplot "RRdias" gegen "RRsyst" 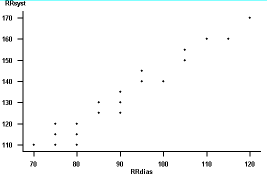
 Applet - dreidimensionale Scatterplots
Applet - dreidimensionale Scatterplots
Zur Untersuchung der Abhängigkeit von zwei oder mehr stetigen Merkmalen dient die Regressionsrechnung. Hier wird nur der Fall der linearen Regression für zwei Merkmale betrachtet.
X (= RRdias) und Y (= RRsys) seien die beiden stetigen Merkmale und es soll Y in Abhängigkeit von X untersucht werden. Oft ist aus dem inhaltlichen Zusammenhang nicht unmittelbar klar, ob man Y in Abhängigkeit von X, oder X in Abhängigkeit von Y untersuchen soll. Wenn man Y in Abhängigkeit von X untersucht, spricht man von der "Regression von Y auf X", wenn man X in Abhängigkeit von Y untersucht, spricht man von der "Regression von X auf Y".
Zur Veranschaulichung trägt man die Daten als Punktwolke in ein Koordinatensystem ein (Abbildung 3.1). Bei der linearen Regression von Y auf X geht man davon aus, dass zwischen den beiden Merkmalen ein linearer Zusammenhang der Form
Y = b0+b1X
besteht. Die Abweichung der tatsächlich festgestellten Wertepaare von der durch die Gleichung beschriebenen Geraden führt man auf den Einfluss nicht erfasster Störgrößen zurück. Es stellt sich die Aufgabe, b0 und b1 vernünftig aus den Daten zu schätzen.
Dieses Problem wurde mathematisch von C. F. Gauß gelöst. Man erhält die Schätzwerte b1 bzw. b0, die aus den Daten mithilfe der Formeln
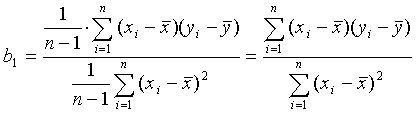
bzw.
![]()
berechnet werden.
Die Gerade
y = b0+b1x
heißt (empirische) Regressionsgerade der Regression von Y auf X; b1, der Anstieg der Regressionsgeraden, heißt (empirischer) Regressionskoeffizient. Außerdem hat sich für den Zähler des Regressionskoeffizienten
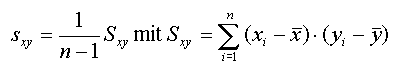
die Bezeichnung "(empirische) Kovarianz von X und Y" eingebürgert. Sie wird analog zur empirischen Varianz
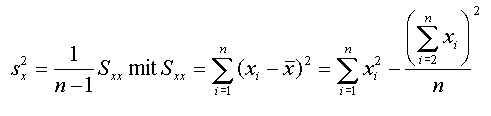
gebildet.
Wer will, kann sich durch Ausmultiplizieren der Quadrate davon überzeugen, dass gilt
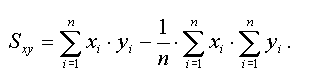
Mithilfe von Varianz und Kovarianz lässt sich die Formel für den Regressionskoeffizienten zu
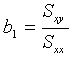
vereinfachen.
Für die Beispieldaten aus Tabelle 3.5 sind alle für die Regression wichtigen Kenngrößen in Tabelle 3.6 zusammengetragen.
Tabelle 3.6: Regressions- und Korrelationsrechnung
RRdias |
RRsys |
||
| (1) |
1185 | (1) |
1940 |
| (2) |
79.00 | (2) |
129.33 |
| (3) |
94525 | (3) |
252950 |
| (4) |
93615 | (4) |
250907 |
| (5) |
910 | (5) |
2043 |
| (6) |
65.00 | (6) |
145.93 |
| (7) |
8.0623 | (7) |
12.0811 |
| (8) |
1.1703 | (8) |
0.5212 |
| (9) |
36.8773 | (9) |
11.5905 |
| (10) |
y=36.88+1.17x | (10) |
x=11.59+0.52y |
| (11) |
154325 | ||
| (12) |
153260 | ||
| (13) |
1065 | ||
| (14) |
0.781 | ||
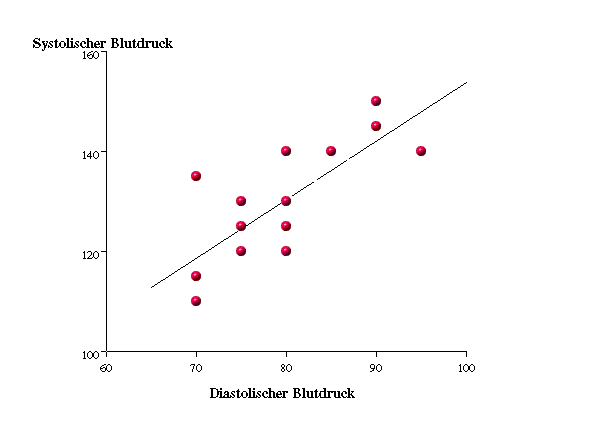
Abbildung 3.2 zeigt noch einmal die Punktwolke mit der berechneten Regressionsgerade.
Abbildung 3.2: Punktwolke und Regressionsgerade - y = 36.88 + 1.17x
 Applet-Korrelation und Regression I
Applet-Korrelation und Regression I
 Applet-Korrelation und Regression II
Applet-Korrelation und Regression II
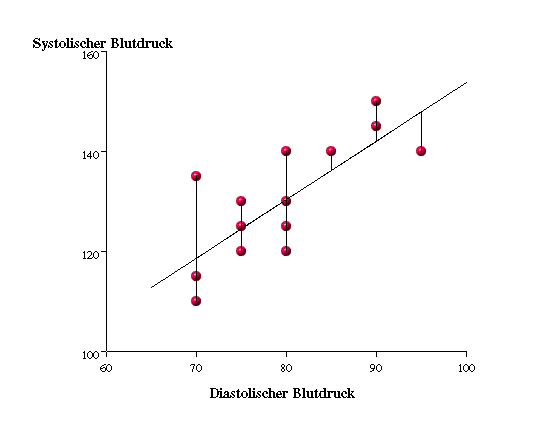
Man kann mathematisch zeigen, dass die so berechnete Regressionsgerade die eindeutig bestimmte Gerade ist, die die Summe der Abstandsquadrate der Punkte von der Geraden minimiert. Hierbei werden die Abstände parallel zur y-Achse gemessen.
Abbildung 3.3: Schema einer linearen Regression - Methode der kleinsten Quadrate
 Applet - Regression Methode der kleinsten Quadrate
Applet - Regression Methode der kleinsten Quadrate
Nach der Durchführung der Rechnung stellt sich die Frage, wie "gut" die ermittelte Gerade zu den Punkten passt oder - etwas spezifischer - wieviel von der Streuung der Y-Werte durch ihre angenommene Abhängigkeit der Korrelation von den X-Werten erklärt wird.
Eine Maßzahl hierfür ist der (empirische) Korrelationskoeffizient r, der durch

oder mit den eingeführten Abkürzungen vereinfacht
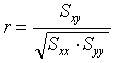
erklärt ist.
Man kann zeigen, dass immer
-1![]() r
r![]() +1
+1
gilt.
Die Grenzfälle r=+1 und r=-1 treten auf, wenn schon alle gemessenen Punkte (xi, yi) auf einer Geraden liegen, wobei die Gerade für r=+1 steigt und für r=-1 fällt. Für r=0 verläuft die Gerade parallel zur x-Achse.
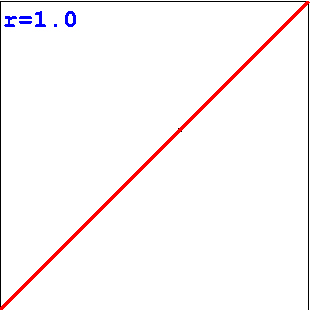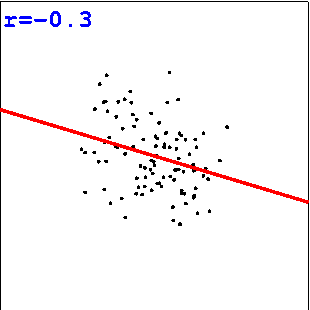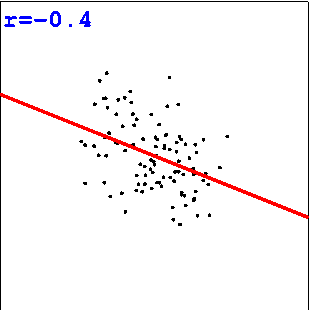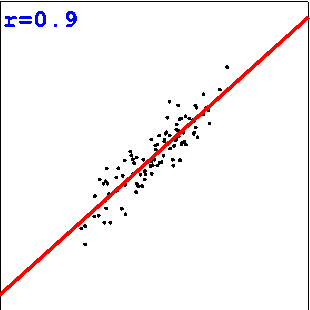
 Übungen zum Schätzen von Korrelationen
Übungen zum Schätzen von Korrelationen
r2, das Quadrat des Korrelationskoeffizienten, heißt Bestimmtheitsmaß. r2 lässt sich interpretieren als Anteil der durch die Regression erklärten Streuung der Y-Werte. Hat man z. B. r=0.7 erhalten, dann ist r2=0.49, d.h., 49 % der Streuung der Y-Werte werden durch die lineare Abhängigkeit von X erklärt. Damit ist r bzw. r2 das gesuchte Maß. Man darf sich aber nicht zu dem Trugschluss verleiten lassen, dass ein r2 nahe bei 1 einen linearen Zusammenhang "beweist". Es wird nur ausgesagt, dass ein angenommener linearer Zusammenhang einen großen Anteil der Streuung der Y-Werte erklärt.
Die bisherigen Rechnungen gelten für die Regression von Y auf X, bei der Y das abhängige und X das unabhängige Merkmal ist. Durch Vertauschung der Rollen von X und Y kommt man zur Regression von X auf Y, bei der X das abhängige und Y das unabhängige Merkmal ist. Die Gleichung der Regressionsgeraden sei
x = a0+a1y.
Ganz analog zu den Rechnungen oben erhält man die Schätzwerte
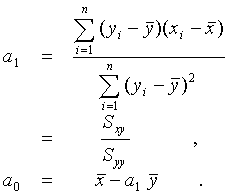
Die Kenngrößen für die Regression von X auf Y sind ebenfalls in Tabelle 3.6 aufgeführt.
Trägt man beide Regressionsgeraden in
das gleiche Koordinatensystem ein, erkennt man, dass sich
die beiden Geraden im Punkt ![]() - dem sogenannten Schwerpunkt - schneiden.
Der Korrelationskoeffizient r ist symmetrisch in X
und Y. Daher erhält man für beide Regressionen
das gleiche r.
- dem sogenannten Schwerpunkt - schneiden.
Der Korrelationskoeffizient r ist symmetrisch in X
und Y. Daher erhält man für beide Regressionen
das gleiche r.
Für r2=1 sind beide Regressionsgeraden identisch.
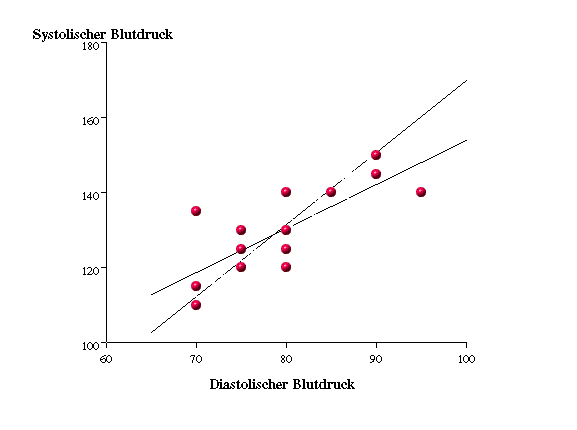
Abbildung 3.4: Punktwolke und Regressionsgeraden - y = 36.88 + 1.17x und x = 11.59 + 0.52y
 Applet - Explorative Datenanalyse -- Datensatz "Blutdruck" - Scatterplot "RRdias" gegen "RRsyst"
Applet - Explorative Datenanalyse -- Datensatz "Blutdruck" - Scatterplot "RRdias" gegen "RRsyst" 
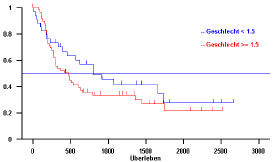
3.4 Schätzung der Überlebensraten nach Kaplan-Meier
In der Medizin werden häufig Merkmale vom Typ einer Überlebenszeit betrachtet. Man versteht darunter Merkmale, die wie eine Überlebenszeit durch ein Anfangs- und ein Enddatum charakterisiert sind.
Beide Angaben sind jeweils durch das Eintreten eines Ereignisses gekennzeichnet. Bei den eigentlichen Überlebenszeiten ist das Anfangsdatum z. B. das Datum der Erstdiagnose einer Erkrankung, das Enddatum ist das Todesdatum. Es kann aber auch das Anfangsdatum das Datum einer Operation, und das Enddatum das Datum der Entlassung aus dem Krankenhaus sein. Die Überlebenszeit ist jeweils die Zeitspanne zwischen beiden Daten.
Man spricht von einer zensierten Überlebenszeit, wenn das Endereignis am Stichtag der Auswertung noch nicht eingetreten ist. In diesem Fall steht für die Auswertung nur eine untere Schranke für die noch nicht bekannte tatsächliche Überlebenszeit zur Verfügung.
Unter der Überlebensrate S(t)
versteht man den Anteil der Individuen, deren Überlebenszeit
größer als t ist (S für engl.:
survival). Es besteht die Aufgabe, diesen Anteil aus den
Daten zu schätzen. Den errechneten Schätzwert
bezeichnet man üblicherweise mit ![]() .
.
Die zensierten Überlebenszeiten bilden
ein Problem bei der Berechnung von ![]() . Ein Verfahren, das es gestattet, die
zensierten Überlebenszeiten sinnvoll einzubeziehen, ist
das Schätzverfahren
von E. Kaplan und P. Meier.
. Ein Verfahren, das es gestattet, die
zensierten Überlebenszeiten sinnvoll einzubeziehen, ist
das Schätzverfahren
von E. Kaplan und P. Meier.
Das Verfahren soll anhand der
Beispieldaten aus Tabelle 3.7 beschrieben werden. Die
Tabelle enthält in Spalte (2) die Überlebenszeiten von
20 Tieren aus einem Tierversuch. Die Überlebenszeiten
sind bereits als Differenz von Anfangs- und Enddatum
ausgerechnet und in Tagen angegeben. Da die Tiere im
allgemeinen nicht alle am gleichen Tag in den Versuch
aufgenommen werden, müssen die Versuchstage für jedes
Tier individuell gezählt werden. Versuchstag 20 für
Tier A kann z. B. für Tier B der Versuchstag 5 sein.
Zensierte Zeiten sind durch "+" gekennzeichnet.
Die Zeiten sind - gleichgültig ob zensiert oder nicht -
der Größe nach geordnet. t0 = 0<t1<t2<
... <tn .
Spalte (3) enthält die Anzahl ni derjenigen Versuchstiere, die den jeweiligen Versuchstag ti lebend erreichen, man sagt auch, die zum Zeitpunkt ti im Risiko stehen.
Diese Zahlen
n1,n2,n3 ...
errechnet man sukzessive mit Hilfe der Angaben in Spalte (4). Dort steht die Anzahl di der zum Zeitpunkt ti eingegangenen Tiere. Immer wenn ti nicht zensiert ist, ist ein Tier eingegangen. Daher ist z. B. d3=0, denn t3=43 ist eine zensierte Überlebenszeit. Zum Zeitpunkt t6=70 sind 2 Versuchstiere eingegangen, d.h. d6=2.
Offenbar gilt
ni = ni-1 - di-1 (i = 1,2,...).
Nach diesen Vorbereitungen besteht die Grundidee des Kaplan-Meier-Verfahrens darin, zunächst für jeden Zeitpunkt ti die bedingten Überlebensraten qi auszurechnen:
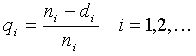 .
.
Das ist der Anteil derer, die den
Zeitpunkt ti überleben, von
all denen, die ihn erreichen. Die qi
werden in Spalte (5) berechnet. Die geschätzte
Überlebensrate ![]() erhält man
durch Aufmultiplizieren aller qi.
Dies ist in Spalte (6) notiert:
erhält man
durch Aufmultiplizieren aller qi.
Dies ist in Spalte (6) notiert:
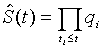 .
.
Tabelle 3.7 enthält aus einem Tierversuch 20 Überlebenszeiten in Tagen. Die Zeiten sind bereits aufsteigend sortiert. An den mit (+) gekennzeichneten Zeitpunkten endet die Beobachtungszeit, ohne dass das betrachtete Ereignis (hier Tod des Versuchstiers) eingetreten ist. Solche am Stichtag der Auswertung noch anhaltenden Überlebenszeiten nennt man zensiert.